音乐始于度量,本于太一
《吕氏春秋· 大乐》
概述
音乐声学是最古老的实验科学之一。毕达哥拉斯(Pythagoras)发现音符的音高与振动弦或管乐空气柱的长度之间的直接关系。这个伟大的发现不光定义了西方音律音阶体系,它也一直是人类最古老的对于自然法则的数学表达。
Levenson[[1]]并且这个信息量丰富却简明的理论可以清楚的描述音乐与科学在各个历史时期的相互作用。符合人类听觉体验中悦耳的、美妙的声音,都基于一根被拉伸的弦的长度的简单比例。这被认为是上帝之手的证据,而不是宇宙中的偶然性。从古希腊时代到牛顿发现万有引力定律和牛顿力学,哲学家和科学家都相信一个由数字和简单形状组合而成的宇宙。在这个宇宙中充满了基于精确分数的音乐——“寰宇之音”。
十九世纪,音乐声学在实验和数学物理的发展中继续占据着中心地位。瑞利勋爵(Lord Rayleigh)的两卷音阶理论的出版使音乐声学的发展达到了顶峰[3],它至今仍为现代声学的几乎所有分支提供理论框架。19世纪声学的发展和对波的理解也为20世纪早期量子力学的发展奠定了概念和数学基础。
关于琴弦震动的物理学研究,如同量子场等式赋予基本粒子质量这种类似弦论的解决方式,可以说是走过了一个轮回。(斯蒂芬·霍金[4])
音乐声学几乎涉及声学理论和实验声学的所有方面。从教学的角度来看,它提供了一个接触整个声学领域的途径。 它可以向任何学年的学生介绍重要的科学知识,毕竟几乎每个人都对某种音乐感兴趣。需要注意的是:如果不去了解听者对声音的感知和解读方式,就不可能全面考虑乐器中和声音有关的各种问题。而这正是大多数科学教学和科研工作中所缺乏的人性维度。音乐声学同时也应该为学生提供无限的机会,博采众长的去了解各种各样的乐器与音乐,古典,民族,现代和世界范围内的风土人情。
它可以向任何学年的学生介绍重要的科学知识,毕竟几乎每个人都对某种音乐感兴趣。需要注意的是:如果不去了解听者对声音的感知和解读方式,就不可能全面考虑乐器中和声音有关的各种问题。而这正是大多数科学教学和科研工作中所缺乏的人性维度。音乐声学同时也应该为学生提供无限的机会,博采众长的去了解各种各样的乐器与音乐,古典,民族,现代和世界范围内的风土人情。
本文的部分内容来自于弗莱彻(Fletcher)和罗辛的《乐器物理学》[[5]]并成为本章讨论的几乎每一个主题的权威性概述和附加参考资料的来源。其他引用来自于Rossing,Moore和Wheeler的《声音科学》[[6]]其中以简明易懂的数学知识提供了最新的研究成果,并描述了更广泛的主题。我们希望将音乐声学将研究这个有趣的话题尽量以通俗易懂的方式进行传播,这需要脱离开僵化的物理教科书。
1 乐器的振动模式
1.1 简正振动模式(Normal wave)
所有的乐器都是通过振动的方式来产生声音的。其中,简正振动方式又称简正模式或简正波(normal wave),是无阻尼系统的一种自由振动模式。其频率称为简正频率。在低频段下,同一系统有多个简正振动可以被激发。这些简正频率可以线性叠加,反过来说一个振动总系统无论有多复杂,都可以分解为简正振动方式的和。
木管乐器、铜管乐器和打击乐器都是直接发出声音。可是小提琴是间接的辐射声音。因为振动弦本身辐射的能量微乎其微。比如电小提琴不插电的话,声音小的像蚊子叫一样很。为了获得更大的声音,来自振动琴弦的能量必须转移到琴体这种更大面积、更有效的辐射表面。至此产振动模式就变复杂了。后续的振动模式涉及到小提琴所有组件的相互作用和振动,如琴弦、琴码、面背板、音柱、琴颈,甚至小提琴体内部的空气。一把小提琴就相当于一个庞大复杂的振动系统,刚才说的各种部件就相当于一个个独立的子系统。每一个子系统都有自己的简正振动模式。
学电的同学可以忽略以上内容,令人赏(ji)心(pi)悦(ge)目(da)的公式为: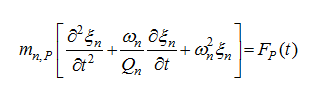
贤者公式解读
其中,有效质量是P点位置的mn,P是根据激发模的动能定义的,n=2fn是在没有阻尼的情况下激励模态自由振动的本征频率(角频率),Qn是描述其阻尼的质量因子。最初,我们考虑点P处的局部驱动力F(t),实际上它可以应用于结构上的任何选择点或分布在整个表面上。
一维弦、实心杆或空气柱在最大位移点处的有效质量为振动系统质量的一半,该系数为正弦空间位移上动能平均值的一半。同样,二维振动物体的有效质量,如小提琴面板或鼓皮,在最大位移位置的质量是其质量的1/4。在位移很小的节点位置附近,有效质量非常大;当模态位移较大时,有效质量很小。
小提琴作用在琴码上的驱动力是由高度非线性的激励机制产生的。相比之下,振动结构的振动通常是线性的,位移与驱动力成正比。然而,当非线性在足够强的激励下变得显著时,几乎所有类型的乐器都会有重要的变化。
在任何持续持续振动的乐器中,振动系统的反馈会产生周期性的驱动力,而这种驱动力通常不是正弦的。然而,根据Fourier定理,任何周期性力都可以表示为正弦变化的谐波部分的叠加,频率是周期重复频率的整数倍。因此,我们可以从任何乐器的振动模式对一系列正弦驱动力的感应响应来考虑任何乐器的振动。
1.2 共振(Resonance)
大家都荡过秋千。当我们掌握好节奏,只需要在秋千到达最高点时轻轻一推,秋千就可以荡得很高。但是如果我们只知道瞎几把推,那荡秋千的人就很难受,秋千也荡不起来。这种当外力的作用(或者另一个振动),和物体本身的振动频率相同时,造成外力(或振动)被放大的现象,就是共振(resonance)。
有耿直的朋友会问,为什么当外部的频率恰当的时候,就可以对物体或者系统引发共振呢?请后排睡着的朋友们和我一起举起双手。我们试着用最自然的状态把整个手臂甩起来,甩的时候请注意不到打到其他同学练。这时候基本不会费什么力气。但是如果我们加快或者减小甩手的频率,那就会变得开始吃力起来。因为当手还在想要往回走的时候,我们因为频率比它高,用的力气已经开始往前。而当手开始往前的时候,我们的力气又要开始往后走了。这个过程里面,一大部分的能量都通过做负功而耗散掉。
但是如果在共振频率上面,当手想要往前的时候,我们给的力气刚好也是往前,手想要往后的时候,给的力也是往后。这样以来,这个力一直对着手臂做正功,使得手臂获得的能量越来越大,振幅越来越大,因此共振也就产生了。对于一端闭合的管状物体,共振会发生在腔体共振频率和它的奇数倍频率上:
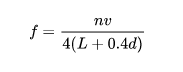
其中f为共振发生的频率,L为腔体长度,d为腔体直径,v为波速,n为正奇数。
1.3 导纳(Admittance)
在声学上导纳定义为一界面(surface)上,例如,任何材料界面,墙、或火箭喷嘴面等,因声波扰动所造成之垂直向扰动速度与界面上声波压力扰动量的比值。数学上,声导纳为一复数值。其实数部分代表当声波传递至界面时,界面是吸收或放出能量予声波;虚数部分则代表声波传递至界面而反射时,时间的延迟现象。因此,声导纳可用来描述一界面之边界条件情形。例如,任何材料,其声导纳之值可用来判断此材料之吸音能力。一完全刚性墙,当声波传递碰到此刚性墙时,会造成声波之完全反射,因此,其垂直向之速度扰动为零,故声导纳为零。一般而言,声导纳与声波传播之频率有关。
贤者公式解读

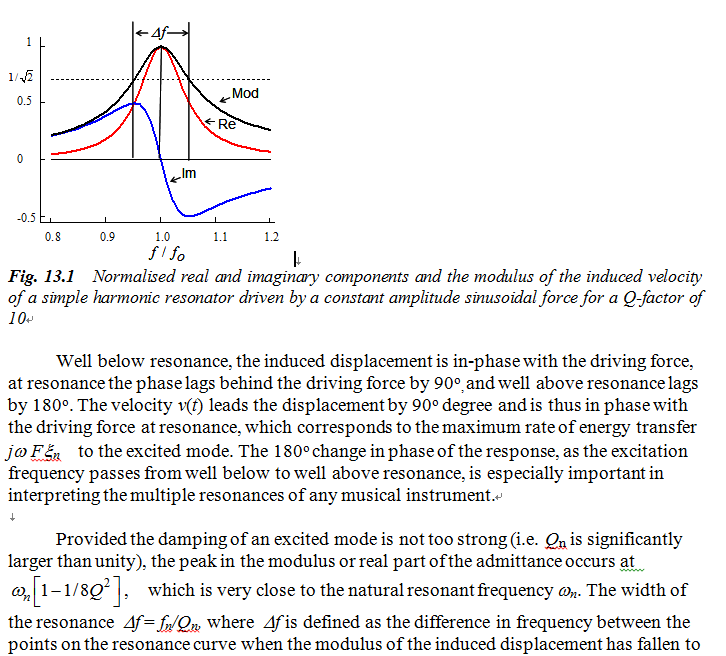
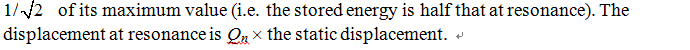
1.4 多重振动模式(Multi-mode Systems)
对于所有具有多种振动模式的乐器,在驱动点P处的导纳可以写作AnP,代表各个独立振动系统的阻抗并联相加。因此,
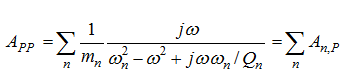
多共振模式乐器的振动响应可通过将测得的导纳与该函数拟合来表征,该函数给出激励点处的有效质量、各激励模式的共振频率和Q值。使用这样的方法[Bissinger]我们可以识别出4 kHz以下小提琴的大约40种振动结构模式。然而,在高频率下,单个共振的宽度超过了它们之间的间距,使得识别单个模式变得越来越困难。更重要的是要认识到阻尼只在单个共振峰周围的相对较窄的频率范围(fn/Q)上才重要。在这些区域之外,与每个振动模式相关联的被动组件继续对导纳作出重要贡献。所有这些振动模式和振动结构影响着小提琴的全局声学特征。
贤者公式解读


2.乐器的声辐射(Radiation from instruments)
虽然乐器的许多振动模式都可以被同时激发,但它们对声辐射的贡献是不同的。这对声音的质量有着重要的影响。本节简要介绍乐器振动模式的声音辐射。
2.1 定义
声辐射(radiation of sound)是指乐器在空气中形成声场的过程。乐器的振动引起周围的空气振动,向远方传播,形成声波和声场。声辐射一方面要研究声源振动时与介质的转化效率,另一方面也要研究声场(有声波存在的区域)的规律。
2.2 声源辐射效率
一个声源振动的能量中有多大的比例转化为声能?这取决于声源和介质的相互作用,主要受如下因素影响。
2.2.1 传播介质
在不考虑乐器在太空中和水下演奏的情况下,以后提到的介质都统一指的是地球标准大气压下的空气。在空气中传播的声速主要受温度影响,次要受空气湿度影响。假设空气温度20摄氏度,空气湿度50%则声速约等于343米/秒。声速公式为:![]()
2.2.2 声辐射强度
主要受声压级(SPL)影响:
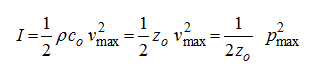
声压级(SPL)相对于2.10-5 Pa或Nm-2的参考声压po以dB为单位进行测量,因此声压级(dB)=20 log10(p/po)
2.2.3 面板声辐射
很多乐器振动的方式都是通过一个二维平面的振动,比如小提琴的面板和鼓面。显然鼓的声辐射性能不如小提琴,这与二维平面的几何非对称性有重要关系。这个比较可能会让打击乐的同学不开心,那就还是用小提琴的面板也依旧成立。当我们去掉了低音梁之后,同一把小提琴的声辐射效率会有显著的降低。
在提琴面板的振动中随着频率的增加,存在着一个临界频率。当面板的相速度小于声波在空气中传播速度的时候,小提琴的声辐射效率较低。当达到2Khz频率时,面板的声辐射效率较高。
2.3 声场对声辐射的影响
声场指的是空间内存在声波的区域。声辐射最主要的性质是其产生的声场的性质,如声场的频率、强度和空间分布等。
2.3.1 球面波(Spherical Waves)
设想在无限大的空间且均匀媒质中有一球状声源,其表面迅速地膨胀和收缩,且表面上的各点作同相位同振幅的振动,向周围媒质辐射的波就是球面波。这种声波是球对称的,即声压的大小仅与离球心的距离有关。任何形状的声源,只要它的尺寸比波长小的多得都可以看作点声源,辐射球面波。
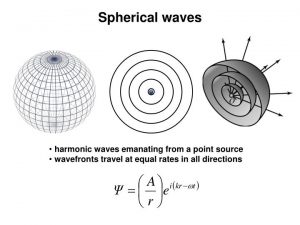
2.3.2 近场与远场
声场中描述压力与粒子速度相关性的三维波动方程:
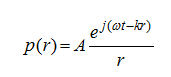
近场就是当其中kr<1。此时压力与声速呈相位正交,不涉及能量的损耗也没有声辐射。相反在远场中(kr>1),声压与声速同相对周围的空气做功。声辐射强度变化为1/r2。例如当频率为340Hz时,距离音源15厘米以内的空间为近场,超过15cm为远场。对于演奏家来说自己听到的声音和观众听到的声音截然不同,这种区别并不止是改变了听起来音量的大小。反过来对于其他乐器的演奏家来说,大部分情况下自己的耳朵都会距离乐器15厘米以上,这意味着自己听到的声音和观众听到的除了音量大小之外并没有其他太多的变化。
2.3.3 指向性与多级源
在低频率下,声波波长通常比声源乐器的物理尺寸大得多(比如琴体的大小),这个阶段可以将声源视为向空间方向均匀声辐射的单独一个点的辐射源。然而,当波长与声源乐器的尺寸差不多的时候,声辐射就有了指向性。这种特性由琴体的几何结构;激励模式;振动模式三方面塑造而成。我们将这种指向性的区别描述为单级;偶极其;四极和高阶多极声源叠加。

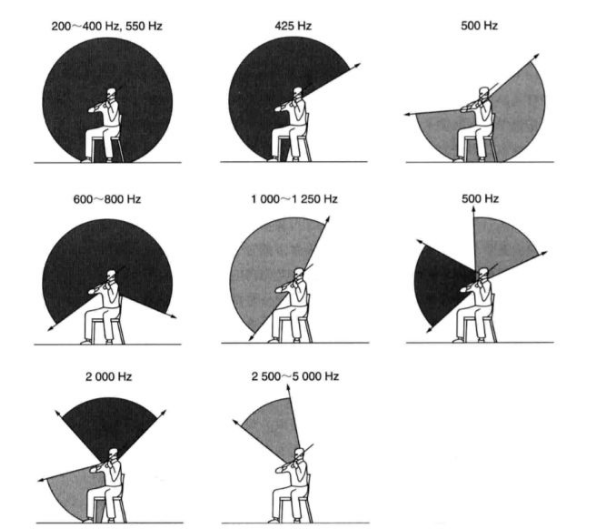
小提琴声音的指向性
3. 解构声音
3.1 乐器的波形
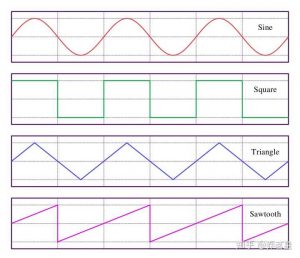
声学上最重要的波形正弦波(Sinusoidal Waves)在音乐声学的领域内并不是是最重要的。这种听起来虽然纯净但是永远干巴巴的声音毫无层次感。除了正弦波,之前我们还提到过另外三种波形:锯齿波、方波和三角波。这三种才是各种乐器发出的波形。
既然之前说过任何声音,无论多么复杂都可以用正弦波的叠加以频谱的方式来描述。那么我们就可以用这种方式人工合成出某种声音。例如下面这段人工合成的锯齿波音频a,同时我们加入了另一段双簧管b在同一音高上的录音用以比较两者听起来到底有什么区别:
两者之间的音质很容易分辨出哪个更好听一点。将上述两端音频进行分析之后可以得到如下结果:
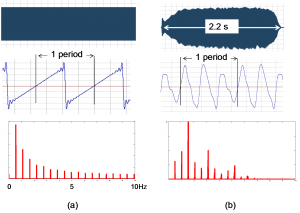
人工合成的声音和真实乐器的声音看起来的区别就是这样的。图中的这些主要的特性决定了音色,他们就是整体包络结构、波形、振幅与频谱。
3.2 傅里叶理论
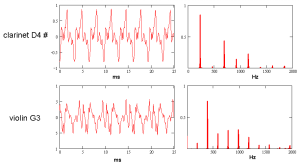 实际的乐器演奏中,情况远比上面那个例子要复杂。波形和频谱从一个音符到下一个音符都会发生显著变化,甚至在一个音符内也会发生变化,尤其是在弦乐器上。尽管波形复杂,任何重复的波形都可以描述为正弦波的线性叠加,其频率是基波的整数倍。下图所示黑管演奏的D#4和小提琴演奏的G3都可以将波形转化为看起来更舒服一点的频谱图:
实际的乐器演奏中,情况远比上面那个例子要复杂。波形和频谱从一个音符到下一个音符都会发生显著变化,甚至在一个音符内也会发生变化,尤其是在弦乐器上。尽管波形复杂,任何重复的波形都可以描述为正弦波的线性叠加,其频率是基波的整数倍。下图所示黑管演奏的D#4和小提琴演奏的G3都可以将波形转化为看起来更舒服一点的频谱图:
如何办到将重复的波形都描述为正弦波的线性叠加?这个频谱图怎么算出来的?这时就需要请到大神傅里叶了。由于这部分比较难理解,除了声学的一些基本概念还需要三角函数和微积分作为基础。希望有兴趣的亲们可以在了解傅里叶理论之前先复习下初中与高中课本内的这部分知识,可以更快速的理解我们未来要经常讨论的频谱图到底是怎么来的。相信这些都是必要的,因为古人云:

图片来自于岛国漫画《漫画傅里叶解析》
- 所谓傅立叶变換无非就是:对一些复杂的函数, 很难用用公式作出解析表达。一些数学家提出,满足一定的条件下可以用一系列的正弦函数逼近那个难以表达的原函数。习惯上,把原函数的变量称为时间变量。而傅里叶变换结果变量,称为频率变量。前者以时间排序,表达的是实际的物理时间过程。后者 以频率排序。表达的是实际物理的结构参数(固有频率)或者,运动的重复性信息(运动周期.)
- 所谓谱:都是按一定的规则排序就称为谱。在计算上实际上就是线性代数的一个列阵(原函数的抽样序列)乘上一个方阵(核函数或称基函数,得到另外一个列阵。(其实任何一个积分变换,在数学上都是一个矩阵乘法,定义不同的方正元素就对应不同的积分变換)前后两个列阵在空间上旋转了90度。
3.2 奔放外一篇 :看不懂可以掐死作者的傅里叶理论解读
前言:
谨以此文献给大连海事大学的吴楠老师,柳晓鸣老师,王新年老师以及张晶泊老师。
傅里叶分析不仅仅是一个数学工具,更是一种可以彻底颠覆一个人以前世界观的思维模式。但不幸的是,傅里叶分析的公式看起来太复杂了,所以很多大一新生上来就懵圈并从此对它深恶痛绝。老实说,这么有意思的东西居然成了大学里的杀手课程,不得不归咎于编教材的人实在是太严肃了。(您把教材写得好玩一点会死吗?会死吗?)所以我一直想写一个有意思的文章来解释傅里叶分析,有可能的话高中生都能看懂的那种。所以,不管读到这里的您从事何种工作,我保证您都能看懂,并且一定将体会到通过傅里叶分析看到世界另一个样子时的快感。至于对于已经有一定基础的朋友,也希望不要看到会的地方就急忙往后翻,仔细读一定会有新的发现。
抱歉,还是要啰嗦一句:其实学习本来就不是易事,我写这篇文章的初衷也是希望大家学习起来更加轻松,充满乐趣。但是千万!千万不要把这篇文章收藏起来,或是存下地址,心里想着:以后有时间再看。这样的例子太多了,也许几年后你都没有再打开这个页面。无论如何,耐下心,读下去。这篇文章要比读课本要轻松、开心得多……
3.2.1. 嘛叫频域:
从我们出生,我们看到的世界都以时间贯穿,股票的走势、人的身高、汽车的轨迹都会随着时间发生改变。这种以时间作为参照来观察动态世界的方法我们称其为时域分析。而我们也想当然的认为,世间万物都在随着时间不停的改变,并且永远不会静止下来。但如果我告诉你,用另一种方法来观察世界的话,你会发现世界是永恒不变的,你会不会觉得我疯了?我没有疯,这个静止的世界就叫做频域。先举一个公式上并非很恰当,但意义上再贴切不过的例子:在你的理解中,一段音乐是什么呢?
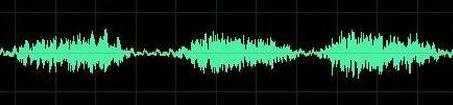
这是我们对音乐最普遍的理解,一个随着时间变化的震动。但我相信对乐器小能手们来说,音乐更直观的理解是这样的:

好的!下课,同学们再见。
是的,其实这一段写到这里已经可以结束了。上图是音乐在时域的样子,而下图则是音乐在频域的样子。所以频域这一概念对大家都从不陌生,只是从来没意识到而已。现在我们可以回过头来重新看看一开始那句痴人说梦般的话:世界是永恒的。将以上两图简化:
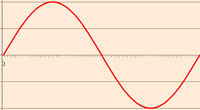

时域 频域
在时域,我们观察到钢琴的琴弦一会上一会下的摆动,就如同一支股票的走势;而在频域,只有那一个永恒的音符。
所(前方高能!~~~~~~~~~~~非战斗人员退散~~~~~~~)以(~~~~~~~~~~~~~~~前方高能预警~~~~~~~~~~~~~~前方高能~~~~~~~~)
你眼中看似落叶纷飞变化无常的世界,实际只是躺在上帝怀中一份早已谱好的乐章。
(众人:鸡汤滚出知乎!)
抱歉,这不是一句鸡汤文,而是黑板上确凿的公式:傅里叶同学告诉我们,任何周期函数,都可以看作是不同振幅,不同相位正弦波的叠加。在第一个例子里我们可以理解为,利用对不同琴键不同力度,不同时间点的敲击,可以组合出任何一首乐曲。而贯穿时域与频域的方法之一,就是传中说的傅里叶分析。傅里叶分析可分为傅里叶级数(Fourier Serie)和傅里叶变换(Fourier Transformation),我们从简单的开始谈起。
3.2.2 傅里叶级数(Fourier Series)
还是举个栗子并且有图有真相才好理解。如果我说我能用前面说的正弦曲线波叠加出一个带90度角的矩形波来,你会相信吗?你不会,就像当年的我一样。但是看看下图:
- 第一幅图是一个郁闷的正弦波cos(x)
- 第二幅图是2个卖萌的正弦波的叠加cos(x)+a.cos(3x)
- 第三幅图是4个发春的正弦波的叠加
- 第四幅图是10个便秘的正弦波的叠加
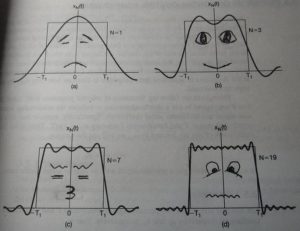
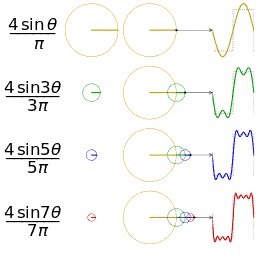
随着正弦波数量逐渐的增长,他们最终会叠加成一个标准的矩形,大家从中体会到了什么道理?(只要努力,弯的都能掰直!)随着叠加的递增,所有正弦波中上升的部分逐渐让原本缓慢增加的曲线不断变陡,而所有正弦波中下降的部分又抵消了上升到最高处时继续上升的部分使其变为水平线。一个矩形就这么叠加而成了。但是要多少个正弦波叠加起来才能形成一个标准90度角的矩形波呢?不幸的告诉大家,答案是无穷多个。(上帝:我能让你们猜着我?)
不仅仅是矩形,你能想到的任何波形都是可以如此方法用正弦波叠加起来的。这是没有接触过傅里叶分析的人在直觉上的
第一个难点,但是一旦接受了这样的设定,游戏就开始有意思起来了。还是上图的正弦波累加成矩形波,我们换一个角度来看看:在这几幅图中,最前面黑色的线就是所有正弦波叠加而成的总和,也就是越来越接近矩形波的那个图形。而后面依不同颜色排列而成的正弦波就是组合为矩形波的各个分量。这些正弦波按照频率从低到高从前向后排列开来,而每一个波的振幅都是不同的。一定有细心的读者发现了,每两个正弦波之间都还有一条直线,那并不是分割线,而是振幅为0的正弦波!也就是说,为了组成特殊的曲线,有些正弦波成分是不需要的。这里,不同频率的正弦波我们成为频率分量。
好了,关键的地方来了!!如果我们把第一个频率最低的频率分量看作“1”,我们就有了构建频域的最基本单元。对于我们最常见的有理数轴,数字“1”就是有理数轴的基本单元。(好吧,数学称法为——基。在那个年代,这个字还没有其他奇怪的解释,后面还有正交基这样的词汇我会说吗?)时域的基本单元就是“1秒”,如果我们将一个角频率为的正弦波cos(
t)看作基础,那么频域的基本单元就是
。有了“1”,还要有“0”才能构成世界,那么频域的“0”是什么呢?cos(0t)就是一个周期无限长的正弦波,也就是一条直线!所以在频域,0频率也被称为直流分量,在傅里叶级数的叠加中,它仅仅影响全部波形相对于数轴整体向上或是向下而不改变波的形状。
接下来,让我们回到初中,回忆一下已经死去的八戒,啊不,已经死去的**是怎么定义正弦波的吧。
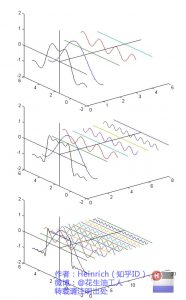
正弦波就是一个圆周运动在一条直线上的投影。所以频域的基本单元也可以理解为一个始终在旋转的圆:
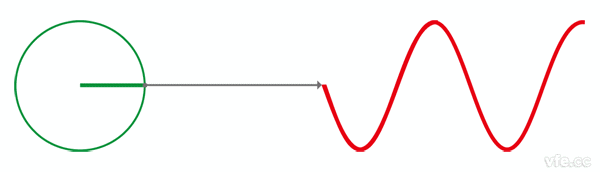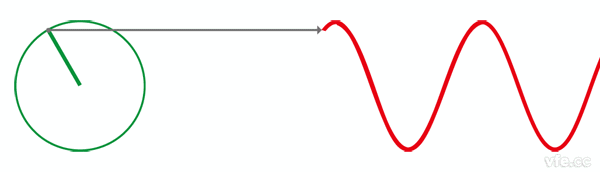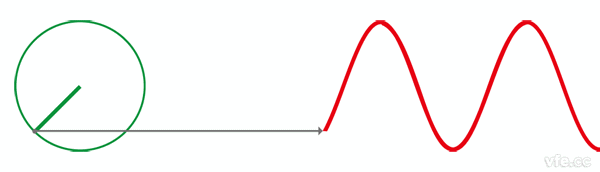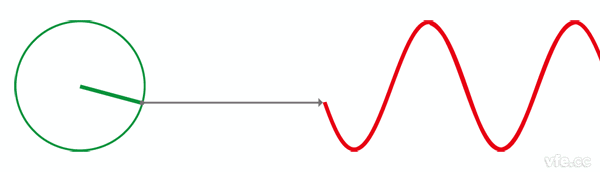
介绍完了频域的基本组成单元,我们就可以看一看一个矩形波,在频域里的另一个模样了: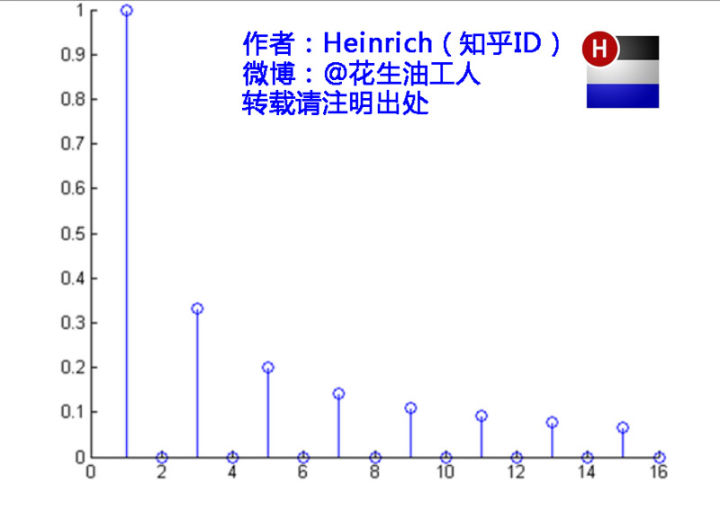
这是什么奇怪的东西?这就是矩形波在频域的样子,是不是完全认不出来了?教科书一般就给到这里然后留给了读者无穷的遐想,以及无穷的吐槽,其实教科书只要补一张图就足够了:频域图像,也就是俗称的频谱,就是——
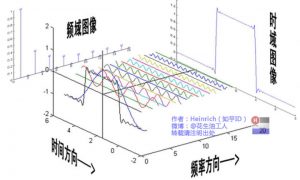

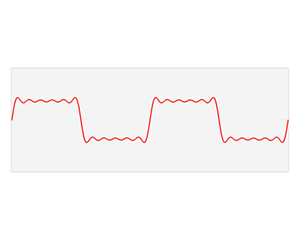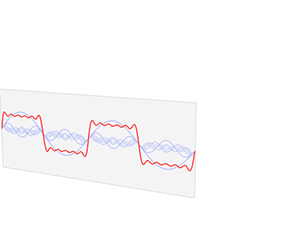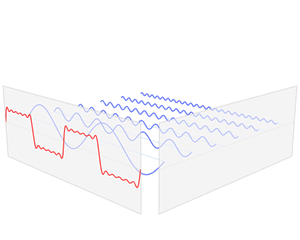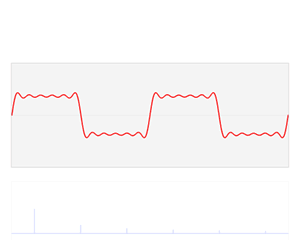
可以发现,在频谱中,偶数项的振幅都是0,也就对应了图中的彩色直线。振幅为0的正弦波。
老实说,在我学傅里叶变换时,维基的这个图还没有出现,那时我就想到了这种表达方法,而且,后面还会加入维基没有表示出来的另一个谱——相位谱。但是在讲相位谱之前,我们先回顾一下刚刚的这个例子究竟意味着什么。记得前面说过的那句“世界是静止的”吗?估计好多人对这句话都已经吐槽半天了。想象一下,世界上每一个看似混乱的表象,实际都是一条时间轴上不规则的曲线,但实际这些曲线都是由这些无穷无尽的正弦波组成。我们看似不规律的事情反而是规律的正弦波在时域上的投影,而正弦波又是一个旋转的圆在直线上的投影。那么你的脑海中会产生一个什么画面呢?
我们眼中的世界就像皮影戏的大幕布,幕布的后面有无数的齿轮,大齿轮带动小齿轮,小齿轮再带动更小的。在最外面的小齿轮上有一个小人——那就是我们自己。我们只看到这个小人毫无规律的在幕布前表演,却无法预测他下一步会去哪。而幕布后面的齿轮却永远一直那样不停的旋转,永不停歇。这样说来有些宿命论的感觉。说实话,这种对人生的描绘是我一个朋友在我们都是高中生的时候感叹的,当时想想似懂非懂,直到有一天我学到了傅里叶级数……

3.2.3 傅里叶级数(Fourier Series)的相位谱
上一章的关键词是:从侧面看。这一章的关键词是:从下面看。
在这一章最开始,我想先回答很多人的一个问题:傅里叶分析究竟是干什么用的?这段相对比较枯燥,已经知道了的同学可以直接跳到下一个分割线。先说一个最直接的用途。无论听广播还是看电视,我们一定对一个词不陌生——频道。频道频道,就是频率的通道,不同的频道就是将不同的频率作为一个通道来进行信息传输。下面大家尝试一件事:
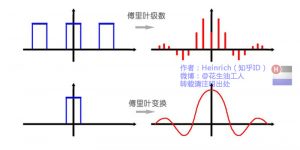
先在纸上画一个sin(x),不一定标准,意思差不多就行。不是很难吧。好,接下去画一个sin(3x)+sin(5x)的图形。别说标准不标准了,曲线什么时候上升什么时候下降你都不一定画的对吧?好,画不出来不要紧,我把sin(3x)+sin(5x)的曲线给你,但是前提是你不知道这个曲线的方程式,现在需要你把sin(5x)给我从图里拿出去,看看剩下的是什么。这基本是不可能做到的。但是在频域呢?则简单的很,无非就是几条竖线而已。
- 所以很多在时域看似不可能做到的数学操作,在频域相反很容易。这就是需要傅里叶变换的地方。尤其是从某条曲线中去除一些特定的频率成分,这在工程上称为滤波,是信号处理最重要的概念之一,只有在频域才能轻松的做到。
- 再说一个更重要,但是稍微复杂一点的用途——求解微分方程。(这段有点难度,看不懂的可以直接跳过这段)微分方程的重要性不用我过多介绍了。各行各业都用的到。但是求解微分方程却是一件相当麻烦的事情。因为除了要计算加减乘除,还要计算微分积分。而傅里叶变换则可以让微分和积分在频域中变为乘法和除法,大学数学瞬间变小学算术有没有。傅里叶分析当然还有其他更重要的用途,我们随着讲随着提。
下面我们继续说相位谱:通过时域到频域的变换,我们得到了一个从侧面看的频谱,但是这个频谱并没有包含时域中全部的信息。因为频谱只代表每一个对应的正弦波的振幅是多少,而没有提到相位。基础的正弦波A.sin(wt+θ)中,振幅,频率,相位缺一不可,不同相位决定了波的位置,所以对于频域分析,仅仅有频谱(振幅谱)是不够的,我们还需要一个相位谱。那么这个相位谱在哪呢?我们看下图,这次为了避免图片太混论,我们用7个波叠加的图。
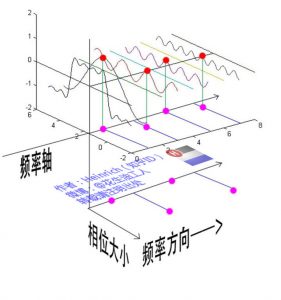
鉴于正弦波是周期的,我们需要设定一个用来标记正弦波位置的东西。在图中就是那些小红点。小红点是距离频率轴最近的波峰,而这个波峰所处的位置离频率轴有多远呢?为了看的更清楚,我们将红色的点投影到下平面,投影点我们用粉色点来表示。当然,这些粉色的点只标注了波峰距离频率轴的距离,并不是相位。
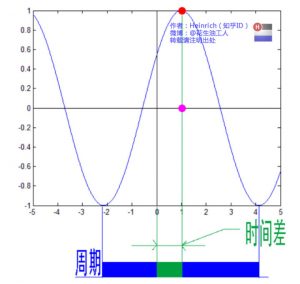
这里需要纠正一个概念:时间差并不是相位差。如果将全部周期看作2Pi或者360度的话,相位差则是时间差在一个周期中所占的比例。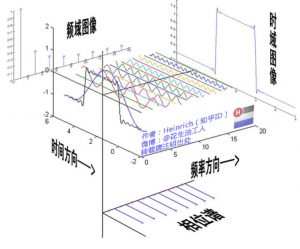 我们将时间差除周期再乘2Pi,就得到了相位差。在完整的立体图中,我们将投影得到的时间差依次除以所在频率的周期,就得到了最下面的相位谱。所以,频谱是从侧面看,相位谱是从下面看。下次偷看女生裙底被发现的话,可以告诉她:“对不起,我只是想看看你的相位谱。”
我们将时间差除周期再乘2Pi,就得到了相位差。在完整的立体图中,我们将投影得到的时间差依次除以所在频率的周期,就得到了最下面的相位谱。所以,频谱是从侧面看,相位谱是从下面看。下次偷看女生裙底被发现的话,可以告诉她:“对不起,我只是想看看你的相位谱。”
注意到,相位谱中的相位除了0,就是Pi。因为cos(t+Pi)=-cos(t),所以实际上相位为Pi的波只是上下翻转了而已。对于周期方波的傅里叶级数,这样的相位谱已经是很简单的了。另外值得注意的是,由于cos(t+2Pi)=cos(t),所以相位差是周期的,pi和3pi,5pi,7pi都是相同的相位。人为定义相位谱的值域为(-pi,pi],所以图中的相位差均为Pi。
3.2.4 傅里叶变换(Fourier Transformation)
相信通过前面三章,大家对频域以及傅里叶级数都有了一个全新的认识。但是文章在一开始关于钢琴琴谱的例子我曾说过,这个栗子是一个公式错误,但是概念典型的例子。所谓的公式错误在哪里呢?——傅里叶级数的本质是将一个周期的信号分解成无限多分开的(离散的)正弦波,但是宇宙似乎并不是周期的。曾经在学数字信号处理的时候写过一首打油诗:往昔连续非周期,回忆周期不连续,任你ZT、DFT,还原不回去。(请无视我渣一样的文学水平……)
在这个世界上,有的事情一期一会,永不再来,并且时间始终不曾停息地将那些刻骨铭心的往昔连续的标记在时间点上。但是这些事情往往又成为了我们格外宝贵的回忆,在我们大脑里隔一段时间就会周期性的蹦出来一下,可惜这些回忆都是零散的片段,往往只有最幸福的回忆,而平淡的回忆则逐渐被我们忘却。因为,往昔是一个连续的非周期信号,而回忆是一个周期离散信号。
是否有一种数学工具将连续非周期信号变换为周期离散信号呢?抱歉,真没有。比如傅里叶级数,在时域是一个周期且连续的函数,而在频域是一个非周期离散的函数。这句话比较绕嘴,实在看着费事可以干脆回忆第一章的图片。而在我们接下去要讲的傅里叶变换,则是将一个时域非周期的连续信号,转换为一个在频域非周期的连续信号。算了,还是上一张图方便大家理解吧:
或者我们也可以换一个角度理解:傅里叶变换实际上是对一个周期无限大的函数进行傅里叶变换。所以说,钢琴谱其实并非一个连续的频谱,而是很多在时间上离散的频率,但是这样的一个贴切的比喻真的是很难找出第二个来了。因此在傅里叶变换在频域上就从离散谱变成了连续谱。那么连续谱是什么样子呢?
你见过大海么?为了方便大家对比,我们这次从另一个角度来看频谱,还是傅里叶级数中用到最多的那幅图,我们从频率较高的方向看。以上是离散谱,那么连续谱是什么样子呢?尽情的发挥你的想象,想象这些离散的正弦波离得越来越近,逐渐变得连续……直到变得像波涛起伏的大海:

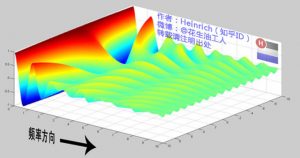
很抱歉,为了能让这些波浪更清晰的看到,我没有选用正确的计算参数,而是选择了一些让图片更美观的参数,不然这图看起来就像屎一样了。不过通过这样两幅图去比较,大家应该可以理解如何从离散谱变成了连续谱的了吧?原来离散谱的叠加,变成了连续谱的累积。所以在计算上也从求和符号变成了积分符号。不过,这个故事还没有讲完,接下去,我保证让你看到一幅比上图更美丽壮观的图片,但是这里需要介绍到一个数学工具才能然故事继续,这个工具就是——
3.2.5 欧拉公式
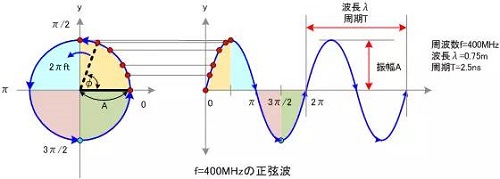
宇宙耍帅第一公式:欧拉公式。虚数i这个概念大家在高中就接触过,但那时我们只知道它是-1的平方根,可是它真正的意义是什么呢?

再坚持一下!你也可以欧拉欧拉欧拉!
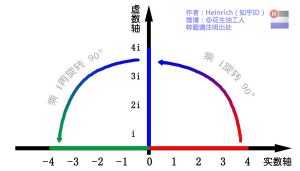
虚数i这个概念大家在高中就接触过,但那时我们只知道它是-1的平方根,可是它真正的意义是什么呢?这里有一条数轴,在数轴上有一个红色的线段,它的长度是1。当它乘以3的时候,它的长度发生了变化,变成了蓝色的线段,而当它乘以-1的时候,就变成了绿色的线段,或者说线段在数轴上围绕原点旋转了180度。
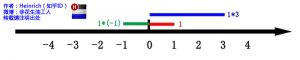
我们知道乘-1其实就是乘了两次 i使线段旋转了180度,那么乘一次 i 呢——答案很简单——旋转了90度。同时,我们获得了一个垂直的虚数轴。实数轴与虚数轴共同构成了一个复数的平面,也称复平面。这样我们就了解到,乘虚数i的一个功能——旋转。
现在,就有请宇宙第一耍帅公式欧拉公式隆重登场:![]()
 这个公式在数学领域的意义要远大于傅里叶分析,但是它成为宇宙第一耍帅公式是因为它的特殊形式——当x等于Pi的时候。
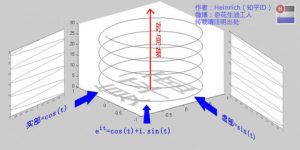
这个公式在数学领域的意义要远大于傅里叶分析,但是它成为宇宙第一耍帅公式是因为它的特殊形式——当x等于Pi的时候。![]() 。经常有理工科的学生为了跟妹子表现自己的学术功底,用这个公式来给妹子解释数学之美:”石榴姐你看,这个公式里既有自然底数e,自然数1和0,虚数i还有圆周率pi,它是这么简洁,这么美丽啊!“但是姑娘们心里往往只有一句话:”臭屌丝……“ 这个公式关键的作用,是将正弦波统一成了简单的指数形式。我们来看看图像上的涵义:
。经常有理工科的学生为了跟妹子表现自己的学术功底,用这个公式来给妹子解释数学之美:”石榴姐你看,这个公式里既有自然底数e,自然数1和0,虚数i还有圆周率pi,它是这么简洁,这么美丽啊!“但是姑娘们心里往往只有一句话:”臭屌丝……“ 这个公式关键的作用,是将正弦波统一成了简单的指数形式。我们来看看图像上的涵义:
欧拉公式所描绘的,是一个随着时间变化,在复平面上做圆周运动的点,随着时间的改变,在时间轴上就成了一条螺旋线。如果只看它的实数部分,也就是螺旋线在左侧的投影,就是一个最基础的余弦函数。而右侧的投影则是一个正弦函数。
3.2.6 指数形式的傅里叶变换
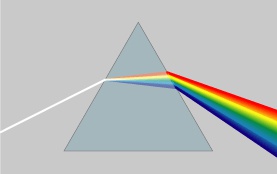 有了欧拉公式的帮助,我们便知道:正弦波的叠加,也可以理解为螺旋线的叠加在实数空间的投影。而螺旋线的叠加如果用一个形象的栗子来理解是什么呢?光波!高中时我们就学过,自然光是由不同颜色的光叠加而成的,而最著名的实验就是牛顿师傅的三棱镜实验:
有了欧拉公式的帮助,我们便知道:正弦波的叠加,也可以理解为螺旋线的叠加在实数空间的投影。而螺旋线的叠加如果用一个形象的栗子来理解是什么呢?光波!高中时我们就学过,自然光是由不同颜色的光叠加而成的,而最著名的实验就是牛顿师傅的三棱镜实验:
所以其实我们在很早就接触到了光的频谱,只是并没有了解频谱更重要的意义。不同的是,傅里叶变换出来的频谱不仅仅是可见光这样频率范围有限的叠加,而是频率从0到无穷所有频率的组合。这里,我们可以用两种方法来理解正弦波:
- 第一种前面已经讲过了,就是螺旋线在实轴的投影。
- 另一种需要借助欧拉公式的另一种形式去理解:
将以上两式相加再除2,得到:
这个式子可以怎么理解呢?我们刚才讲过,e^(it)可以理解为一条逆时针旋转的螺旋线,那么e^(-it)则可以理解为一条顺时针旋转的螺旋线。而cos(t)则是这两条旋转方向不同的螺旋线叠加的一半,因为这两条螺旋线的虚数部分相互抵消掉了!举个例子的话,就是极化方向不同的两束光波,磁场抵消,电场加倍。这里,逆时针旋转的我们称为正频率,而顺时针旋转的我们称为负频率(注意不是复频率)。
好了,刚才我们已经看到了大海——连续的傅里叶变换频谱,现在想一想,连续的螺旋线会是什么样子:想象一下再往下翻:
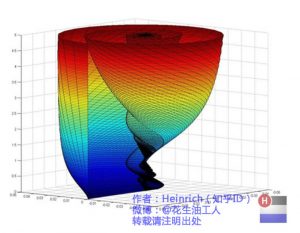
是不是很漂亮?你猜猜,这个图形在时域是什么样子?
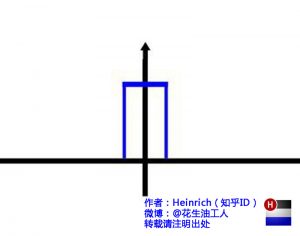
哈哈,是不是觉得被狠狠扇了一个耳光。数学就是这么一个把简单的问题搞得很复杂的东西。顺便说一句,那个像大海螺一样的图,为了方便观看,我仅仅展示了其中正频率的部分,负频率的部分没有显示出来。如果你认真去看,海螺图上的每一条螺旋线都是可以清楚的看到的,每一条螺旋线都有着不同的振幅(旋转半径),频率(旋转周期)以及相位。而将所有螺旋线连成平面,就是这幅海螺图了。
好了,讲到这里,相信大家对傅里叶变换以及傅里叶级数都有了一个形象的理解了,我们最后用一张图来总结一下:
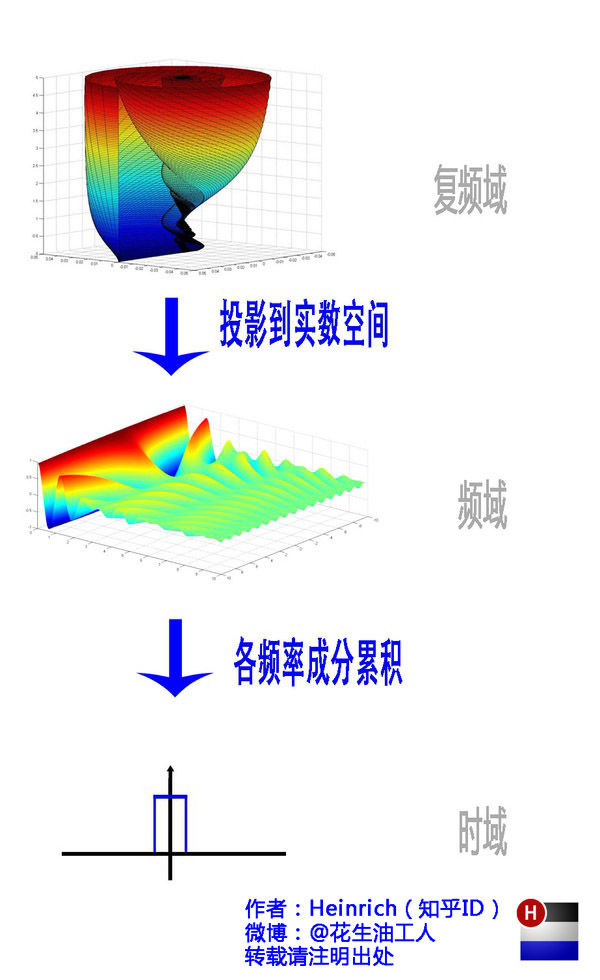
以上,傅里叶的故事终于讲完了。
4. 数字录音(Digital Recording)
现在几乎所有的声音都是用模数转换器(ADC)数字记录的。这将不断变化的模拟输入信号转换成数字流,数字流可以数字形式记录在计算机或光盘上。有耿直的朋友问黑胶不香吗?我就好模拟信号这一口。这么说其实也没错关于音乐喜好的问题均不应该使用到好还是不好这种词。更恰当的比喻可能是豆腐脑吃甜的还是咸的这一永恒问题,咸甜两教派之间都应该放下成见求同存异。至于为什么用数字录音?简单说就是:好用,好听,便宜。
4.1 声音采集与存储
 采样,指把时域或空间域的连续量转化成离散量的过程 。对声音的采样常用麦克风等设备将声音信号转换成电信号,再用模/数转换器将电信号转换成一串用1和0表示的二进制数字(数字信号)。我们每秒对声音采样上万次,获得上万个按照时间顺序排列的二进制数字。于是,我们就将连续变化不断的声音转化成了计算机可储存并识别的二进制数字。如win10的关机音效音由84700个不同的数字组成。 其中的一段数字如下:(二进制数字已转换为十进制):… 413, 263, 137, 15, -124, -253, -369, -463, -511, -545, -587, -632, -678, -701, -687, -659, -623, -579, -539, -473, -380, -282, -162, -35, 78, 211, 341, 430, 499, 548, 551, …如果用图像的形式表示该音频,则如右图:(横轴是时间,纵轴为振幅,两个图像分别代表左右声道。)
采样,指把时域或空间域的连续量转化成离散量的过程 。对声音的采样常用麦克风等设备将声音信号转换成电信号,再用模/数转换器将电信号转换成一串用1和0表示的二进制数字(数字信号)。我们每秒对声音采样上万次,获得上万个按照时间顺序排列的二进制数字。于是,我们就将连续变化不断的声音转化成了计算机可储存并识别的二进制数字。如win10的关机音效音由84700个不同的数字组成。 其中的一段数字如下:(二进制数字已转换为十进制):… 413, 263, 137, 15, -124, -253, -369, -463, -511, -545, -587, -632, -678, -701, -687, -659, -623, -579, -539, -473, -380, -282, -162, -35, 78, 211, 341, 430, 499, 548, 551, …如果用图像的形式表示该音频,则如右图:(横轴是时间,纵轴为振幅,两个图像分别代表左右声道。)
4.1.1 采样频率
采样频率指录音设备在一秒钟内对声音信号的采样次数。采样频率越高,声音的还原就越真实越自然。目前主流的采样频率有22.05KHz、44.1KHz、48KHz三种。22.05 KHz为FM广播的声音品质,44.1KHz为理论上的CD声音品质。48KHz为人耳可辨别的最高采样频率。直观理解如下图:一段连续的声音——等间隔采集——最终采集结果
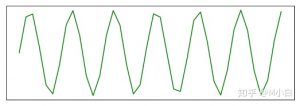
如下图可见,采样频率越高,我们获得的声音品质越好。
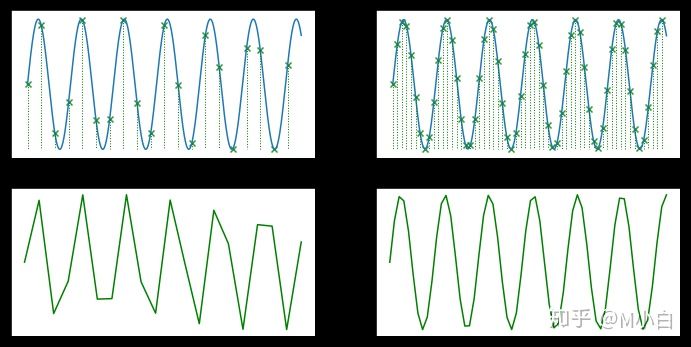
4. 1.2 量化位数
我们不可能获得所有时间下声音的强度,因此声音是等时间间隔、离散采样的。同样,采样获得的数据不可能无限的精确,如数字为63.2222222….,这无法在计算机中储存。因此,采样获得的数据同样也是离散的。量化位数是音频文件的另一个参数。量化位数越大,声音的质量越高。常用的量化位数有8位、16位和32位。量化位数指用几位二进制数来存储采样获得的数据。量化位数为8即指用8位二进制数来存储数据,如00010111还是之前的例子,有一段正弦声波,假设量化位数为3,即存储的数据只有000/001/010/011/100/101/110/111这8种可能。现在,还是等距离采样,不过采样的点只能落在右图最近的红线上。
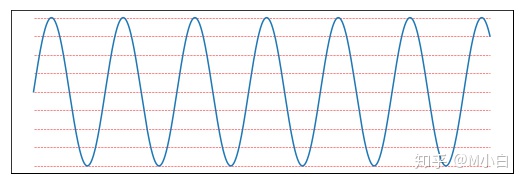

由下图可见,量化位数越大,声音效果越好。
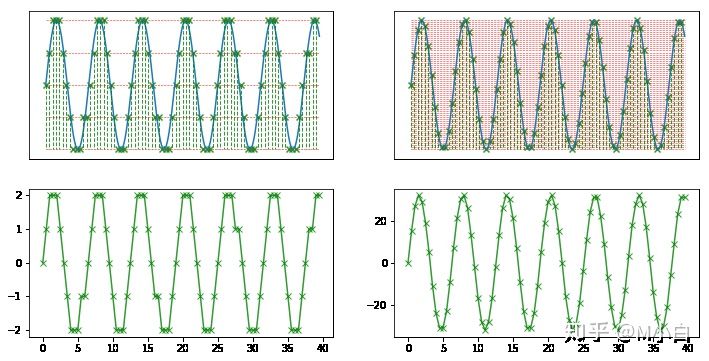
4. 1.3 声道数
声道分为单声道与双声道。单声道即为左右耳听到的声音相同。双声道两耳听到的信息不同。相同的声音时间、采样频率和比特率的情况下,双声道文件的存储空间是单声道的两倍。但其会给人空间感,游戏和电影中常采用双声道,可达到“听声辨位”的效果。示例声音如下:

4.2 音频格式
首先要分层定义,搞清楚调制方式,编码方式,封装格式等的层次关系,才能正确认知这些字母到底是个啥意思。
4.2.1 调制方式(Modulation)
模拟音频要经过数模转换,才能变成数字信号,转换方法有很多,目前主要的调制方式分两大类:
- PCM (Pulse-Code Modulation) 8~f64bit 8k~1.536MHz 1~8Channels: 用于音乐记录与回放的PCM是什么时候开始的已经无从考究了,但我们清楚的是,1980年,索尼和飞利浦发布了CD-DA红皮书规范,制定了16bit/44.1kHz 74min的规格。没错索粉们,就是索尼的工程师嫌40kHz的LPF太难做又嫌飞利浦的48kHz装不进120mm的盘中,才搞了一个210²这么诡异的数字,让我们这些年在跟SRC的斗争中消磨了不少工程师的大好青春。那么74分钟的规格是怎么来的呢?那是史诗级录音——1951年富特文格勒的拜罗伊特版贝九(企鹅评鉴三星带花)的时长。既然是Code,那么就要有Code的时间和Code的方式,采样率定义了Code的时间基准,而位深定义了Code的量化精度。当时的16bit能提供大约94dB的理论信噪比和20kHz的理论频响,而从30多年前的CD-DA到现在的Hi-Res Audio甚至DXD (32bit 352.8kHz/384kHz),PCM的规格越来越高,现在的理论参数已经远超硬件能够实现的程度了。
- PDM (Pulse-Density Modulation) 1bit 2.8224~45.1584MHz 2~8Channels: 很多人没有听说过PDM,但是对PWM (Pulse-Width Modulation)一定不陌生,如PWM调速的风扇,PWM调光的AMOLED等等,其实PWM只是一种脉冲频率固定的特殊的PDM。索尼和飞利浦于1995年发布的DSD (Direct Stream Digital) 格式,正是他们新推出的SACD的编码格式,也是一种特殊的1bit-PDM,即每个周期只有一次脉冲,且负载周期恒定。与PCM相对,PDM音频是直接靠某一时刻前后一段固定时间的脉冲频率来表示该时刻的电平高低。但索尼发布之后,才发现,原来DSD64的高频相噪是如此的可怕,但是当提升到128fs并且以更多的bit (如5~6bit)为单位进行调制的时候,DSD会真正变得无比强大,这就是为什么现代的Σ-Δ型DAC都做成了Multi-bit SDM 。扯得有点远,具体想了解的话,我还可以专门写一篇关于PCM,PWM,PDM,SDM的对比。
4.2.2 编码方式:
经过调制成为数字信号之后,就要考虑通过什么样的编码方式写成文件了。编码分为无压缩编码,无损压缩编码,以及有损压缩编码,这里主要介绍前两种。
- AIFF (Audio Interchange File Format) .aif .aiff 8~32~f64bit 8k~1.536MHz 1~8Channels:这是苹果于1988年发布的开源的音频编码规范,是一种大端序的Linear PCM。许多人以为这是苹果抄袭WAV自己搞的一个小众版WAV,其实他比WAV更加古老,这个规范已经28年没有更新变动了。用过iPod/iDevice的人都知道,AIFF是可以携带元数据的,能够带上艺术家,唱片,流派,甚至封面等ID3信息。
- WAV (Waveform Audio File Format) .wav .wave 8~32~f64bit 8k~1.536MHz 1~8Channels:这是1991年微软和IBM由RIFF规范扩展来的音频规范,与CDA和AIFF一样都为Linear PCM,可以说就是小端序版本的AIFF。因为Windows系统的巨大成功,WAV成为了从上至专业录音棚,下至消费者终端最通用的标准无压缩音频格式。因为其LPCM的性质,在非音频领域WAV的位深,采样率和通道数几乎没有限制。但和AIFF不同的是WAV不携带元数据。
- DSDIFF (DSD Interchange File Format) .dff 1bit 2.8224~22.5792MHz 2~6Channels:这是飞利浦方面定义的DSD交互格式,类似于PCM中的WAV/AIFF,支持多声道,不支持元数据。
- DSF (DSD Streaming Format) .dsf 1bit 2.8224~22.5792MHz 2Channels:这是索尼方面定义的DSD流媒体格式,类似于PCM中的立体声WAV/AIFF,只支持双声道,支持元数据。
- SACD-ISO (Super Audio CD Image File) .iso 1bit 2.8224MHz 2~6Channels:这是索尼PS3旧版本用户们通过破解方式将SACD光盘的映像抓取下来形成的文件类型。里面一般包含着未压缩的DSD原码,可能只含有双声道DSD,也可能还含有5.1声道DSD。有一些ISO甚至包含元数据,但规范并不统一。
Lossless Encode无损压缩编码
- ALAC (Apple Lossless Audio Codec) .m4a 8k~32bit 8~384kHz 1~8Channels:2004发布。一开始是苹果独享的不开源编码,2011年苹果将其开源。压缩率大约在58%~60%,CPU资源消耗介于FLAC和WV之间,没有纠错功能。本以为会随着随身听和数字音乐的发展成为iTunes售卖无损音乐的载体,没想到直到开源iTunes也没有卖无损的意思。
- APE (Monkey’s Audio) .ape 8~24bit 8k~192kHz 1-2Channels: 2000年发布。这是最早从音乐论坛/资源网站开始流行的盗版无损音乐格式。优点是压缩率高,大约为WAV的55%左右(16bit/44.1kHz的CD规格,下同),半开源,由EAC抓轨伴随生成的log会使人信服为真无损。缺点是算法较为复杂,CPU编解码所需要的资源几乎一样,而且远高于其他主流无损编码,没有纠错功能。
- FLAC (Free Lossless Audio Codec) .flac 8~32bit 8k~384kHz 1~8Channels: 2001年发布。这是另一大盗版无损音乐格式,当然,大部分正版无损音乐也是这个格式。优点是全开源,算法较为简单,解码对于CPU资源消耗最少。缺点是压缩率较低,大约为WAV的57~62%大小,没有纠错功能。
- WV (WavePack Lossless) .wv .wvc 8~32~f32bit 8k~384khz 1~8Channels: 1998年发布。这是一个非常有意思的无损编码。把.wv后缀名改为.exe之后它会变成一个自解压文件,运行可以自行解压成WAV音频。同时支持有损模式,并通过.wvc修正文件和有损.wv文件一起还原成无损.wv文件,实际上能支持超高采样率(16.77MHz)与多达256声道,只是我们目前还用不到。缺点是编解码不比APE轻松多少,而压缩率也只有56~58%左右。优点是有纠错功能,可以用空白静音填补丢失或损坏的数据。
- WMA (Windows Media Audio Lossless) .wma 8~24bit 8k~96kHz 1~6Channels:2003年发布。是微软的专利编码方式。压缩率在58%左右,CPU资源消耗大约相当于中档的WV,没有纠错功能。
- DST (Compressed DSD Format) .dst 1bit 2.8224~22.5792MHz 2~6Channels:这是目前已知的唯一一种DSD压缩格式,编码与解码都需要占用非常多的CPU资源。但压缩率非常高,能达到50%左右。这种格式还能携带元数据,并支持多声道。
External Links
- Lorem ipsum dolor sit. “Vivamus quis mi eget justo porttitor eleifend” gloriathemes.com – November 2, 2010
- 知乎同学M小白 数字录音原理
- Donec porttitor purus sit. “Integer porta dolor sit amet maximus rhoncus.” gloriathemes.com – April 10, 2013
- Sed convallis leo aliquam. “In at sapien quis ante ullamcorper porttitor.” themeforest.ney – July 21, 2012
References
Donec aliquam auctor tortor, non malesuada magna consectetur vitae. Nam condimentum justo metus, ac varius neque molestie eget. Aliquam ultricies eros viverra, vulputate turpis tincidunt, tempor lacus. Mauris euismod metus finibus sagittis tincidunt. Donec a augue viverra, porta metus non, congue metus. Nulla tincidunt purus non pharetra elementum. Aliquam fringilla elit ac felis consequat, ut viverra urna porta. Nunc malesuada quam risus. Mauris pellentesque pellentesque porta. Vivamus euismod vulputate tortor. Aenean quis pellentesque nibh consectetur vitae. Nam condimentum justo metus, ac varius neque molestie eget. Aliquam ultricies eros viverra.
- Lorem ipsum dolor sit. (18th ed., 2015)
- Consectetur adipiscing elit. (18th ed., 2015)
- Donec porttitor purus sit.
- Sed convallis leo aliquam.
- Donec eu nisl volutpat. (18th ed., 2015)
- Fringilla orci id, porta quam. (18th ed., 2015)
- Morbi non lectus vitae mauris. (18th ed., 2015)
- Ultrices pretium vitae non erat.
- Nulla consequat arcu vitae. (18th ed., 2015)
- Lorem ipsum dolor sit. (18th ed., 2015)
- Consectetur adipiscing elit. (18th ed., 2015)
- Donec porttitor purus sit.
- Sed convallis leo aliquam.
- Donec eu nisl volutpat. (18th ed., 2015)
- Fringilla orci id, porta quam. (18th ed., 2015)
- Morbi non lectus vitae mauris. (18th ed., 2015)
- Ultrices pretium vitae non erat.
- Nulla consequat arcu vitae. (18th ed., 2015)
- Sed convallis leo aliquam.
- Donec eu nisl volutpat. (18th ed., 2015)