曲木为直终必弯,养狼当犬看家难。墨染鸬鹚黑不久,粉刷乌鸦白不坚。蜜饯黄莲终需苦,强摘瓜果不能甜。好事总得善人做,哪有凡人做神仙。
——打狗年就有
概述
终于,我们进入到了正题。如果有同学是按照顺序一直看到这里的话,恭喜你们这很不容易。好消息是把前面的章节都看的“很有精神!”的话,再来看提琴的振动原理就会容易理解得多了。让我们打起精神!再接再厉。
在这一章中,如果网管鼻血还没流干的话还将继续为同学们找一些直观的视频和动图帮助大家理解。更重要和令人激(tou)动(yun)万(mu)分(xuan)的是我们将用数学与物理学描述提琴在拨弦、拉弦和击弦上产生的声音。这将包括演奏者激发琴弦振动的不同模式,通过桥将振动弦的能量传递到乐器主体的声辐射结构振动,以及声学环境对这种声音的调整作用。虽然声音的产生是基于相对简单的结构的振动,如琴弦和面背板,但正是这些结构之间的相互作用,使其中的物理学远远超出了入门教科书的范围,从而产生提琴特有的声音。
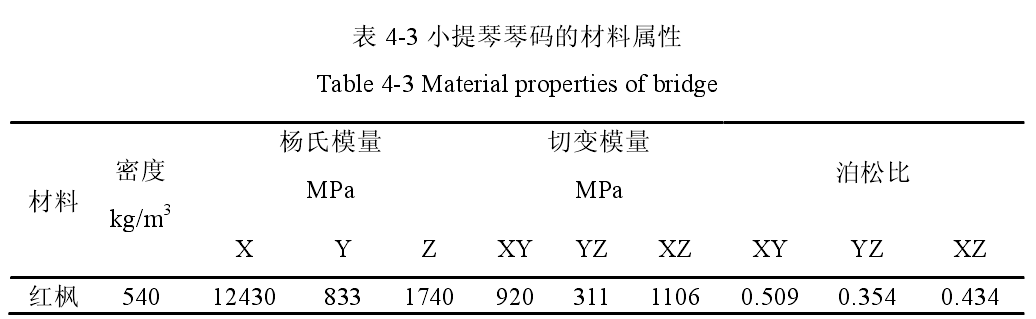
 对于一把正在拉动琴弦的提琴来说,声音是由一个复杂的自激励循环多子系统产生的。这个系统包括乐器、演奏者和声学环境和听众。如右图中所示。琴弦的音质和音准都是由演奏者用左手弦的音准和音准来控制的。此外,通过左手控制音符的音调和右手控制琴弓的手指都有声学之外的直接的触觉反馈。演奏者和听者对声音的感知也同时受到客观存在的声学和主观上大脑处理耳朵中感觉器官所接收声音的方式的强烈影响。所有这些因素都与决定乐器发出的声音的感知质量有关。然而,为了易于从物理上了解所涉及的各种机制,我们可以先把这个复杂的系统产分成一个个子系统(例如琴弦振动;琴码与琴体)来考虑小提琴的声学特性。然而,重要的是不要忽视这样一个事实:任何乐器发出的声音都会涉及到所有这些子系统的相互作用,更重要的是,演奏者的技术才激发和控制最终着声音的产生。
对于一把正在拉动琴弦的提琴来说,声音是由一个复杂的自激励循环多子系统产生的。这个系统包括乐器、演奏者和声学环境和听众。如右图中所示。琴弦的音质和音准都是由演奏者用左手弦的音准和音准来控制的。此外,通过左手控制音符的音调和右手控制琴弓的手指都有声学之外的直接的触觉反馈。演奏者和听者对声音的感知也同时受到客观存在的声学和主观上大脑处理耳朵中感觉器官所接收声音的方式的强烈影响。所有这些因素都与决定乐器发出的声音的感知质量有关。然而,为了易于从物理上了解所涉及的各种机制,我们可以先把这个复杂的系统产分成一个个子系统(例如琴弦振动;琴码与琴体)来考虑小提琴的声学特性。然而,重要的是不要忽视这样一个事实:任何乐器发出的声音都会涉及到所有这些子系统的相互作用,更重要的是,演奏者的技术才激发和控制最终着声音的产生。
1.琴弦的振动
1.1 重要性
 琴弦是小提琴声音的源头,这也是研究提琴声学最基础,最重要,最有挑战,也是最容易被忽视的一个环节。从制造的角度上来说的话,制造琴弦的难度要远高于制作一把小提琴。众所周知琴弦决定小提琴的音高。在同样长度下,由于材质和粗细的差异所以产生了不同的音高。小提琴琴弦的两端是静止不动的,所以当同一条琴弦振动时会产生振幅相同,频率(音高)相同但方向相反的两个正弦波。这两个正弦波的叠加时形成的波叫驻波。
琴弦是小提琴声音的源头,这也是研究提琴声学最基础,最重要,最有挑战,也是最容易被忽视的一个环节。从制造的角度上来说的话,制造琴弦的难度要远高于制作一把小提琴。众所周知琴弦决定小提琴的音高。在同样长度下,由于材质和粗细的差异所以产生了不同的音高。小提琴琴弦的两端是静止不动的,所以当同一条琴弦振动时会产生振幅相同,频率(音高)相同但方向相反的两个正弦波。这两个正弦波的叠加时形成的波叫驻波。
1.2 琴弦振动类型
琴弦有四种振模式:横向振动、纵向振动、扭曲振动和倍频振动。其中,虽然纵波和扭曲波物理上角度也扮演着重要的角色。但从音乐的角度上考虑最重要的振动模式是横向振动阵型。例如纵向波如果是声音的主要的构成时,这是小提琴初学者杀鸡的时候发出来的声音。在这部分的知识储备中我们将主要用到声学巨头德国科学家亥姆霍茨的琴弦振动理论。
1.3 亥姆霍茨(Helmholtz)琴弦振动理论
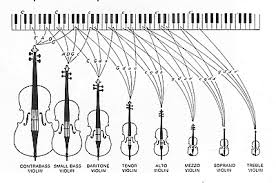
尽管许多物理学家和大多数音乐家直觉上将弦上的波与“教科书”物理学中的正弦波联系在一起,但实际上,拉弦、拨弦或击弦的振动是截然不同的。然而,由于这类波是重复的,从傅里叶定理可以看出,所有这些解都可以描述为正弦波分量的和。然而,拨弦、弓弦和击弦的运动更容易用波动方程的亥姆霍兹解来描述。在考虑实际琴弦与支撑结构的相互作用之前,我们首先考虑具有完全刚性端部支撑的理想弦上正弦和Helmholtz振型的最简单情况:拨弦与拉弦两种模式
上述模型动起来是酱婶儿的:
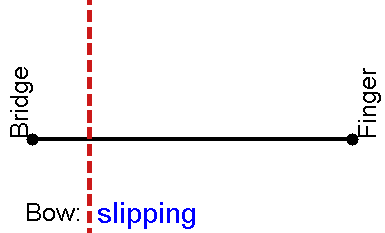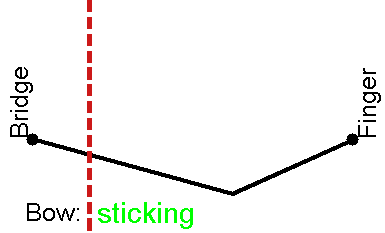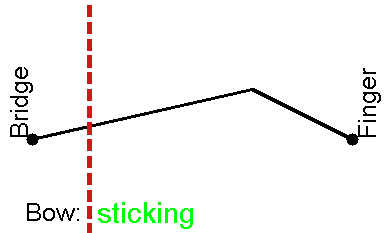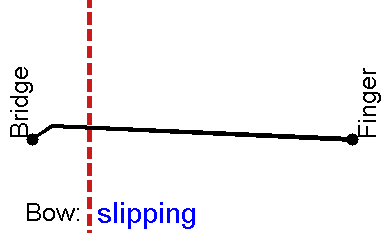
琴弓上小钩子拉扯琴弦是酱婶儿的:
琴弦动起来之后是酱婶儿的:
1.4 琴弦发展史
当小提琴刚发明的时候,只有一种琴弦可以用:以动物肠器做的琴弦,羊肠通常是首选。十九世纪末期,小提琴E弦开始改用全钢丝弦,主要原因是羊肠弦高频区线容易断弦。而用全钢丝弦就没有这个问题。有些演奏家很乐意改用全钢丝E弦,有些则持续抗拒。这种争论持续了上百年。有一种说法是由于接二连三的战争,导致羊肠材料取得困难,不得不改用全钢丝弦。(难道是因为打仗没有其他好吃的?)这种说法的真实性有待考证。众所周知战争结束后现代养殖业迅速恢复到了战前水平。无论是在制弦业发达的英国还是古老的东方,动物肠器都是一种民间需求量很大且易于获取的食材。芯弦在20世纪中期出现,这种新对的技术在羊肠弦及钢弦间找到一个平衡点,合纤芯弦不受气候影响,运弓反应快,容易生产。更符合常识与逻辑的一种可能是小提琴弦的发展随着材料学与金属冶炼技术的进步而不断进化发展。
视频:舌尖上的羊肠弦
2. 琴码(Bridge):
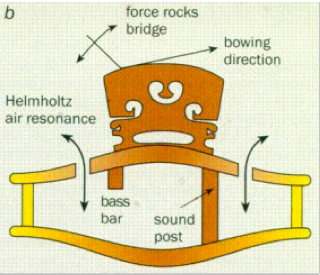
许多弹拨和击弦乐器,例如钢琴或吉他,都使用很低的实心琴码来支撑弦。他们的琴码并不承担向面板传递能量的功能,作用只是防止琴弦打品。对于中国的两弦小提琴二胡来说也是如此,它的握持和弹奏是为了使琴弓激发垂直于而不是平行于支撑琴桥和弦的拉伸蛇皮膜的弦振动。竖琴的琴弦固定在成角度的音板上;因此,弦平面中的横向弦振动直接耦合到支撑音箱的垂直振动(Fletcher和Rossing [5,§11.2])对这类乐器来说,琴码的声学功能微乎其微。小提琴包括提琴家族的琴码对于声学的贡献至关重要。常有制琴老司机教导我们说:“琴码,是一把琴的灵魂。”将一把小提琴琴弦调整到标准音高的情况下,四条琴弦会产生共计约30公斤的强大张力;而在将琴码固定好之后,通过琴码脚施加在面板上的垂直于面板角度的压力会增加到46公斤。(琴弦入射角度13-15度水平地面)
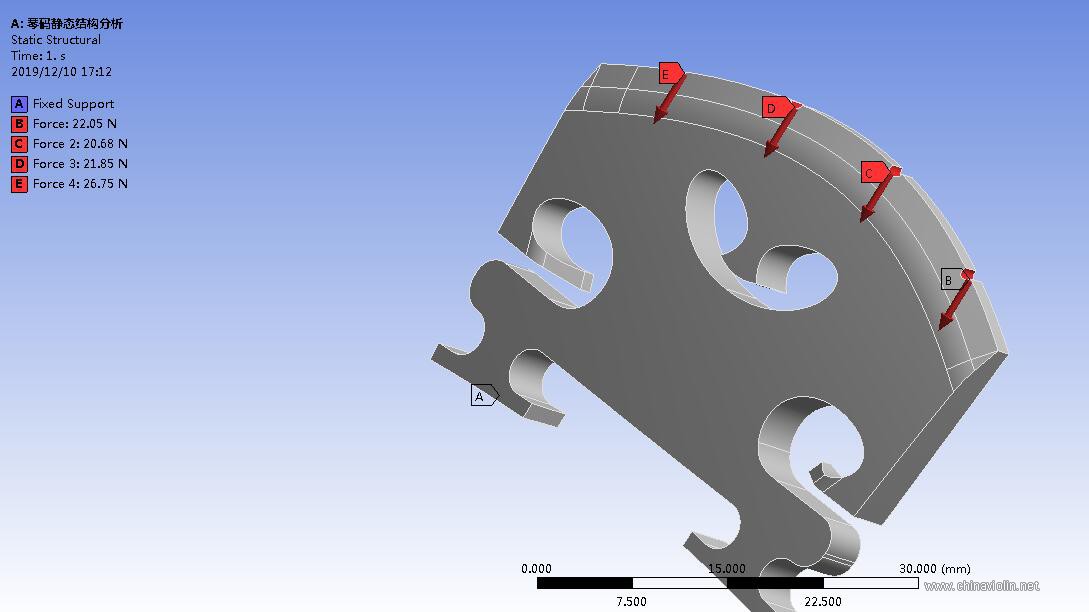
四条琴弦对琴码的应力设置
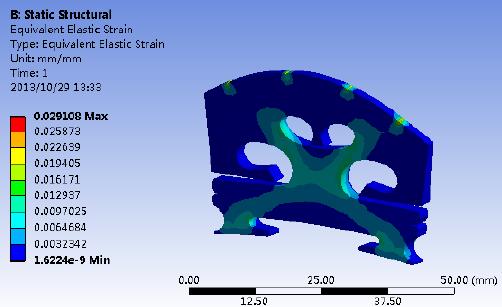
琴码的静力学应力结构分析
2.1 琴码振动特征模式与频率:
下图是小提琴和大提琴桥的最低阶横向振动模态和频率。最左边的箭头代表琴弦的振动方向:
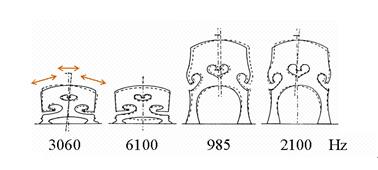
Reinicke指出,最低阶的小提琴琴码共振,通常在3千赫左右,振动的模式是琴码上半部围绕其腰部的旋转运动(像个跳舞的小人)。由支撑在琴码顶部的振动弦引起的旋转运动导致两个琴码脚以这样的方式作用在面板上。下一个重要的共振频率约为6khz,振动模式是琴码作为一个整体在垂直于面板的水平面上做上下跳动,一个人跳起来两只脚同时踩在地面上那样作用于面板。大提琴码很长,这导致了两个低频的扭曲振动振模式,共振频率在1和2千赫左右,这两种模式都通过两只琴码脚施加在面板上。来自琴弦振动的纵向力也可以诱导垂直于其平面的琴码运动(倍频振动模式),但诱导的运动相当小,通常不被视为有音乐意义。
不太规范和严谨的形容一下的话,请同学们想象一下幼儿园的时候玩跷跷板的经历。琴码在第一阶3khz左右振动的模式就是酱紫。两只琴码脚以这样的方式将来自于琴弦的振动传递到面板上。而到了6khz的时候,琴码的振动模式更像是一个人原地跳起双脚同时落地的样子。下图是网管用ANASYS求的解:区别在于琴码脚是否设置了刚性约束条件。


平时没事喜欢玩有限元仿真的同学可以使用如下的材料参数,或者直接去读华南理工张承忠博士的相关论文。
2.2 琴码振动简化模型
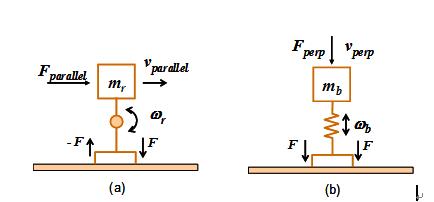
Cremer详细介绍了小提琴和大提琴码与琴体耦合作用的研究。描述了几种较为复杂的琴码与琴体耦合振动模态,并对各种可能的振动模态进行了描述。然而,如下图所示小提琴琴码的主要共振模式可以通过两个自由度的机械模型表示每个振动模式来非常简单地建模,有效质量从琴码顶部通过两个琴码脚到达面板的能通过旋转或垂直弹簧来表示。琴码下半部相对较轻的质量和增加的刚度只会轻微地扰动面板的共振频率,因此作为第一近似可以忽略不计。可以选择耦合弹簧的有效质量和强度来再现小提琴(或大提琴)琴码的前两个振动模式的振动特性,这两个振型控制着小提琴的声学特性。而有了这样的简化模型也是所有后续更深入研究的基础。
在低频,远低于任何共振频率时,琴码将作为一个刚体振动。在面板施加少量附加质量、惯性矩和刚度,这又只会稍微扰动支承壳结构的振动频率。与小提琴桥相比,大提琴桥额外的相对高度使振动的琴弦能够在更大的面板上施加更大的力。如何在增加耦合以增强低频强度的同时,又不会使其变得如此强烈,以至于产生麻烦的wolf-note问题,这两者之间存在微妙的平衡。
2.3 琴码共振峰(Bridge Hill):
琴码做出的种种上述行为使得其像一个滤波器或者效果器一样,起到重塑音色的作用。我们发现有一个有待考证说法是小提琴的设计是为了模拟女高音歌唱家的音色。而琴码的这个设计和对音色的重塑的结果可以使小提琴整体在3000Hz左右的频段产生一个明显的共振峰,这与女高音的声学频谱特征具备一致性。间接的印证了这个小提琴设计初期的音色塑造理念。自20世纪80年代初以来,人们就知道,由于琴码的共振特性,高质量的小提琴尤其是名古琴在2-3kHz左右的频率下振动更好。我们现在称之为“琴码共振峰”,一把提琴是否具备这个频段的共振峰可以成为一种声学数据上衡量小提琴质量的参考,直接与之相对应的是提琴在演奏厅环境的远传性能。而其他用于室内乐演奏的提琴或交响乐队节奏组用琴,和一些质量不好的小提琴则不具备这一特征。
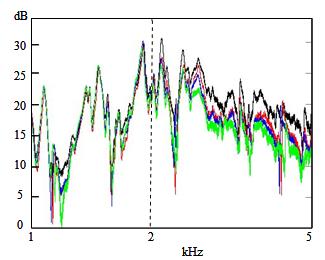 Reinicke和Cremer都强调了琴码共振对小提琴声音和导纳测量的重要性,传统上通过使用与面板平行的外力在琴码顶部激励小提琴来实现。(例如铅笔敲击琴码顶部)近年来,这个问题引起了新的兴趣,Jansson将其称为Bridge Hill(BH)特征。右图显示了Woodhouse对许多把琴琴码导纳模数的测量结果。这些琴码质量各不相同,但在约2kHz下具有相同谐振频率。在琴码共振附近观察到一个很强但相当宽的整体波峰。请注意,随着桥体质量的增加,导纳明显降低,高于琴码共振。在通过峰值时,导纳相位也有一个相关的90度变化。
Reinicke和Cremer都强调了琴码共振对小提琴声音和导纳测量的重要性,传统上通过使用与面板平行的外力在琴码顶部激励小提琴来实现。(例如铅笔敲击琴码顶部)近年来,这个问题引起了新的兴趣,Jansson将其称为Bridge Hill(BH)特征。右图显示了Woodhouse对许多把琴琴码导纳模数的测量结果。这些琴码质量各不相同,但在约2kHz下具有相同谐振频率。在琴码共振附近观察到一个很强但相当宽的整体波峰。请注意,随着桥体质量的增加,导纳明显降低,高于琴码共振。在通过峰值时,导纳相位也有一个相关的90度变化。
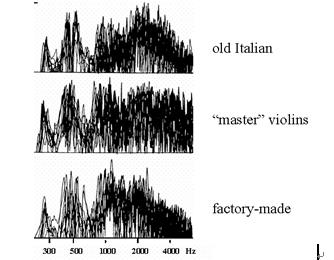 关于BH特征的证据还可以在Dünnwald的叠加测量中看到,大量高品质的名古琴,意大利现代“大师”琴和工琴的声音输出作为琴码顶部正弦输入力的函数,如图右图所示。这些测量有一个令人惊讶的结果是,现代大师琴明显缺乏这样的特征,可能是因为所选琴的琴码共振和面板共振的有效质量变化更大。通过对700多把小提琴的声辐射测量,Dünnwald提出,在1.5至4千赫的宽频带内存在大量强的声共振是一种真正优秀的小提琴显著特征之一。琴码在解释这样一个峰值以及在较高频率下的响应降低的影响显然很重要。
关于BH特征的证据还可以在Dünnwald的叠加测量中看到,大量高品质的名古琴,意大利现代“大师”琴和工琴的声音输出作为琴码顶部正弦输入力的函数,如图右图所示。这些测量有一个令人惊讶的结果是,现代大师琴明显缺乏这样的特征,可能是因为所选琴的琴码共振和面板共振的有效质量变化更大。通过对700多把小提琴的声辐射测量,Dünnwald提出,在1.5至4千赫的宽频带内存在大量强的声共振是一种真正优秀的小提琴显著特征之一。琴码在解释这样一个峰值以及在较高频率下的响应降低的影响显然很重要。
Woodhouse重新讨论了小提琴琴码与琴体之间的耦合问题以及波峰的起源。一个简单的理论模型表明,峰值取决于许多因素,如琴码的有效质量、主要振型和共振频率及提琴的多共振特性。为了演示琴码的整体效果而不必考虑某一把具体的琴的详细振动响应。Woodhouse在简化模型基础上进行了扩展以描述琴码的耦合,为小提琴的振动模式提供了一个更现实但仍然简化的模型。这使他能够搞明白各种涉及琴码的参数对一把琴整体声学特性的影响,提出了小提琴制作者可以通过各种方式改变琴码的特性来优化小提琴的音色,尽管这始终是个人品味的问题,而不是科学定义的问题。
我们需要注意的是琴码在控制小提琴或大提琴的声音方面的重要作用经常被忽视,即使是许多制琴老司机也忽视了这一点觉得把琴做好就完事了。事实上,Cremona小提琴之所以能发出如此值钱的声音,其中一个原因就是他们运用了高超的技巧来调整琴码的质量、细节形状和配件(以及音柱的位置),以优化音质。
经常提到简化模型到底是干嘛的?
虽然样子都不太高大上,但每一个简化模型可能都是学者所追求的终极目标。科学从来就不是一种试图把人忽悠瘸了的学说,相反科学的研究方法总是尽量用最简单的模型去创造一个管用就好的可应用的理论。现代科学提供的是描述我们世界的一个个模型,他们并不完美并且仍有很多还没搞清楚的地方。但是只要一个模型容易理解,管用并且比之前的还要好上那么一点的解释观测事实,做出预测并可以被验证的话我们就只管用就好了。
科学,并不会提供一个“绝对真理”。玄学与宗教才会。
3. 音柱(SOUND POST)与低音梁(BASS BAR)
 在提琴家族中,音柱以不对称的位置支撑在面板和背板之间,如右图所示。 其中也可以看到,低音梁沿面板低音侧纵向延伸。 音柱和低音梁为乐器增加了机械强度,帮助它承受了有角度的琴弦通过琴码传递到面板上产生相当大的向下的力,在小提琴上这个力可以达到10千克。
在提琴家族中,音柱以不对称的位置支撑在面板和背板之间,如右图所示。 其中也可以看到,低音梁沿面板低音侧纵向延伸。 音柱和低音梁为乐器增加了机械强度,帮助它承受了有角度的琴弦通过琴码传递到面板上产生相当大的向下的力,在小提琴上这个力可以达到10千克。
音柱对声音质量的影响是如此之大,以至于法国人将其称为小提琴的灵魂(又是灵魂,还有哪个不是灵魂)。 它的声学功能是让面板和背板通过连接的方式一起振动(直接耦合)。此外还附加了机械约束,也可以让琴弦与琴体一起振(使平行于面板平面的琴弦振动激发简正模式:面板与背板的非对称和对称振动模式的线性组合。)
音柱在中世纪的提琴和其他早期乐器中就已经出现。 古代乐器中的Celtic crwyth使用两个不同长度的琴码脚有效结合了琴码与音柱的功能。这种既是琴码也是音柱的设计也用在了古老的希腊乐器Rebec中。


4. 琴体(BODY)
很多同学估计就是奔着这儿来的,这其实也没错。虽然动不动就这也灵魂那也灵魂什么的,但某种意义上那些都没有琴体重要。因为,那些可拆卸替换的组件换一个并不难。但换琴的话,Hum…

制琴师对于音色的设计主要通过调整琴体上的每一个细微的环节。这些细微的差别在我们实际听起来的时候差别是明显的。这也是为什么意大利黄金时期的的传世名古琴售价过亿,而一些现代工厂流水线出品的小提琴售价只有一百块的原因。(这个问题有待进一步讨论)琴体在这种情况下变成了一个主体,占据小提琴整体声学性能的主要部分。通过激光多普勒测振仪,现在我们可以用最直观的方式了解到小提琴的琴体到底是在怎样振动的。下面请欣赏至今活着的最贵制琴师Sam Zygmuntowicz在科研团队的帮助下使用Polytec激光多普勒测振仪为大家带来的Antonio Stradivari 1715 “Titian”的振动观测结果。(特大好消息,Strad3d数据包打折了,不用499,399。现在登录Strad3D.org只要40刀你就可以拥有全套数据包。朋友还等什么,买它!买它!)
前方高能预警分非战斗人员退散
4.1 新的研究方法:有限元仿真(FEM)
当我们讨论提琴特征频谱数据、振动模式还有一些A0,B1+,B1-神马的时候。我们究竟在说些什么?后排的同学别跑,这次我们直接上干货结论,下面的动画可以用最简单直接的方式了解这些复杂的概念。简单来说那些概念与参数都是用于来描述一把琴在不同阶段的多种振动模式。比如,在不同的频率下有时候琴体作为一个整体是弯曲振动,有时候是扭腰振动,还有的时候像心跳一样做泵式的振动。(细思极恐琴果然是活的,这是要成精了)好了,选修课的同学们动画能看明白的话可以直接下课了。提琴振动的主要原理,琴体的各种特征振动模式与相应频率都在这小段动画里了。
Colin E.Gough教授首次证明了自由板模型和全琴装配壳模型之间的声学模态关系和他们之间的相互作用原理。
毕竟,科学与新技术的进步是用来更高更快更强的(偷懒与省事)。随着强大的计算机和有限元分析软件的出现,我们可以计算出小提琴1 kHz以下的有代表性的前20个简正振动模态的振型与频率。在这样的计算下我们看到了各种各样的振动模式,琴的每个部分确实都在一定程度上参与了振动。(果然都是灵魂)这些模式可以通过使用Chladni板振动(两百年前撒盐大法)、激光全息术(Polytec有钱人大法)和模态分析技术的直接实验观测到。可喜可贺的是,激光多普勒测振仪与有限元仿真分析的新技术让我们这样的小白免于遨游书海可以用最直观的方式了解到关于提琴声学里那些各种各样的概念都实际代表着什么。更重要的是,依靠更先进的技术我们终于有机会建立提琴作为一个整体的简化模型了。而低频区的几个特征频谱其实也是本章节将主要讨论的概念,它们在很大程度上决定了一把琴的音色。留下来的同学请把桌子清理下,接下来我们按惯例需要把琴拆成一片片的进行详细的分析。
提琴声学中的神奇女侠哈金斯自20世纪60年代开始,对提琴进行了大量声学测量与量化。她的激励方式采用了正弦波发生器非接触式,得到面板和背板的自由共振频率,配合Chladni撒盐大法对振动节点线进行了观测与判定。同时她还搜集整理了350年来关于提琴声学的宝贵文献资料自己编辑后出版了两卷论文集《Research Papers in Violin Acoustics, 1975-1993: With an Introductory Essay, 350 Years of Violin Research》。为之后的提琴声学研究者提供了基础文献,对提琴声学做出了重要的贡献。

但是新的问题还在等着我们去挑战:面板背板在完成了全琴的装配后受多种应力的影响,其振动模态会发生改变。哈金斯的研究结果无法得到单独调试的面板背板与装配好的全琴之间振动频率变化的关系。而这才是制琴师最感兴趣的问题,可并没有得到一个靠谱的说法。至今,在传统提琴制作工艺中,制琴师只能通过用手掰面板两侧与首尾来感受材料的弹性模量,用敲击面板发出的声响来决定对面板不同区域薄厚的销切处理。我们要干就要干最关键的问题,在右图中描述的是面板与背板,从没有侧板的振动模态和装配好侧板之后的振动模态和他们之间的转化关系。刚才拆碎了的琴体,被按照顺序从简到繁的组装起来:

- 图左边代表的是面板与背板自由状态的前八阶振动模式(琴做到这里连F孔还没开呢,所以面背板是一样的)我们将其简称为板模型。
- 图右边代表的是将面板背板与侧板装到一起后的振动模式,我们将其简称为壳模型。
- 图下边是一种强刚性强互相作用下的振动模式,我们将其简称为钢板壳模型。
- 之后的内容中,我们还会把壳模型开音孔,此时的模型我们简称开孔壳模型
- 最后我们会加入音柱,此时的模型我们称为真·壳模型。(就是一开始给大家看的动画)通过这种方式我们可以一步步的从简入繁的顺序下了解小提琴是如何振动的。
4.2 板模型:只有两块板
哈金斯板模型的原理:图1中所示的面板是没有f孔的,所以背板和面板的振动模式基本相同。由于两者的拱形轮廓存在细微差别,因此在哈金斯描述中的Mode3和mode 4需要重新排顺序。这些模式代表的是弯曲波的模式,首先由索菲·热尔曼(1816)用数学方法描述。她指出,弯曲波涉及板的曲率或弯曲的空间变化,而不是平面外的z轴位移。因此,得到的波动方程是空间坐标中的四阶,而不是更常见的流固二阶方程波动方程。因此,板的弯曲波解有两种:板边界内常见的二维半波长正弦波驻波解和板边界附近的指数阻尼驻波解。(看到此处网管在流鼻血)这种振动模式同样存在于F孔边缘和音柱与面背板的接触末端。
板模型不同振动模式之间的主要区别:图1中左侧哈金斯的8个mode中,7种mode都需要在没有边界约束(侧板)的情况下才能充分振动。其中只有Mode 5的振动模态中在板内有驻波(不依赖边缘的振动)。Mode 5频率的增加依赖于边界驻波数量的增加。随着该区域附近驻波的增加,Mode 5 频率随之增加。
4.3 钢板壳模型
请自行想象用钢板做面背板和侧板然后把他们焊死在一起的状态,我们将其简称为钢板壳模型。侧板支撑强度逐渐增加的有限元仿真计算中,这种情况下随着侧板支撑强度的增加,整琴体的振动频率迅速增加。增幅远高于常规木制琴模型。这一现象可以更明显的解释了侧板的声学功能,其对面板的约束与限制增加壳模型的振动频率。
4.4 壳模型:加了侧板但是在真空下状态
声音在琴体上产生的顺序:从低频开始,板模式的振动首先出现在下音孔处的大面积区域;随频率逐渐增加,振动区域逐渐转移到上音孔上方。这个趋势同样出现在合琴后的壳模型中。从低频开始面板首先产生上述振动的顺序,当频率增高这种振动趋势开始出现在更厚更重的背板上。当到达10khz全琴不同区域都出现更小面积的局域波,波长近似的局域驻波产生了更多共振。音孔下区域与音孔上方区域的板材料弹性决定了这部分的振动性能。同时,上述局域波通过侧板的链接作用穿过腰部与F孔到达琴中央部位。而这里也是一开始,弓-弦振动通过琴码激励出这些高频振动的位置源头。至此,完成了一次循环。
侧板在壳模型中的耦合作用:在面背板振动模态基本一致的板模式中,两块板扣起来应该是在做相反方向的一致的振动。(镜像对称)为什么在用侧板合在一起之后就出现了不对称的情况?而在壳模型中还没有加入音梁音柱等这些会引起非对称振动的因素,此时的壳结构是各方向上都对称的状态。原因在于壳模型中的面背板边缘被侧板约束,原有的单一物体固有频率振动模式现在变成了组件振动模式,此时在相反方向的振动频率会迅速增加。频率的迅速增加意味着需要更多的势能来承担侧板对于面背板边缘振动在相反方向上的伸展与抑制作用。相比之下,相同方向的振动频率只有在侧板张力的作用下有微弱的增加。因为组件振动模式下,组件之间的边缘已经被粘合到一起,会在相同方向上同时发生位移。这种耦合作用快速的提升了板的振动频率。在这种耦合状态下的面板背板的振动会在不同方向上呈强相关性,而在相同方向上呈弱相对关系。以上解释了侧板的强度对自由振动模式下面背板振动方向的影响。
最重要的呼吸模式B1-的诞生:壳模型中侧板耦合影响着最重要的提琴振动模式B1-呼吸模式和B1+弯曲模式的。众所周知,这两种振动模态耦合后就是总会被提到的B1-和B1+。再次回到需要敲黑板画重点的图1. 中间的曲线图表描述了这种重要的呼吸模式(更像心脏的跳动的状态)是如何形成的。在壳模型下,呼吸模式由板模型下面背板合起来在相反方向的振动模态(应该就是mode 5);面背板在准刚性vd模型下垂直角度的弹跳模式(面背板受侧板边界约束在初始振动下的刚性体振动模态);交互形成。两者量级改变呈强相关性,形成强耦合状态。曲线图表中随着侧板耦合强度的增加,面背板准刚性体的弹跳模态频率逐渐增加(td与Lr)。与mode 5的频率曲线接近但不发生耦合。这时就会像一对耦合振荡器中出现的情况一样,没有发生耦合的频率曲线趋势产生了逆转,如红色加粗曲线所示。当侧板耦合强度在曲线上处于非耦合状态且不相交的情况下,原有的标准振动模态会分裂成弹跳模态和面背板mode5的耦合振动模态两种振动模态。两者在正反两方向上拥有相等的振动能量。当耦合强度高于代表一致性的那条虚线时,低频的振动模态(左右)被平稳的转化成了壳模型的呼吸模态(上下)。这时的侧板的耦合强度中只存在少量的拉伸作用。虽然这个阶段的呼吸模态频率仍低于mode 5,但在增加了角块和尾块后频率可以得到迅速的增加。这种模态的转化,让一个装配后的琴体具备最大化接近板模型的自由状态振动频率。由于对于提琴升学性能重要的呼吸模式只涉及很少的边缘运动,所以有人开始尝试寻求使用钉式固定侧板与面板的方法而不需要使用胶粘合。因为即使这样,面板仍然可以沿着边缘做横向与纵向的自由运动。
弯曲模式 B1+:相比之下,另外一种弯曲模式(B1+)来自于在相同方向上振动的哈金斯mode2 和mode 3.经过耦合后的壳模型的弯曲模式具备和板模型相似的振动频率和一样的振动方向。(通常差别在2个半音之内)这导致了模态转换后的变量很小,频谱特征分析中的声辐射峰值也很小(这就是难以被测到的原因?)。这种耦合后的模式也没有像B1-那样受到准刚性频率升高的影响。当B1+与准刚性模态的两条曲线相交时,并没有出现方向性改变和分裂。最初其最低频率由侧板诱发成为内外振动模式阶段,然后mode 3和mode 4被平稳的转化成相反方向的振动模态(见视频1中的anticlastic bending)。壳模型下的B1+保留了板边缘的大面积位移。
虽然这些模式图有点复杂,但它们还是可以展示出小提琴的振动模态是如何从最开始的哈金斯板模型模态如何转化为壳模型的模态,并与准刚性振动模态发生交互作用的。由此产低频下壳模型的振动模态还是比较简单的形状。The b1– breathing, and both the ld longitudinal and tdlb lower bout transverse and tdub upper bout transverse diploe mode (not illustrated)都精确的展示出符合预期的在反方向上振动模态,局部的约束或牵制作用出现在上述模态的周围。cbr and b1+ bending modes在边缘保留了较大位置的位移区域,即使在高频区这也可以清晰的将原有板模型的振动模态与其进行关联。
4.4 开孔壳模型:只开了音孔别的还没有
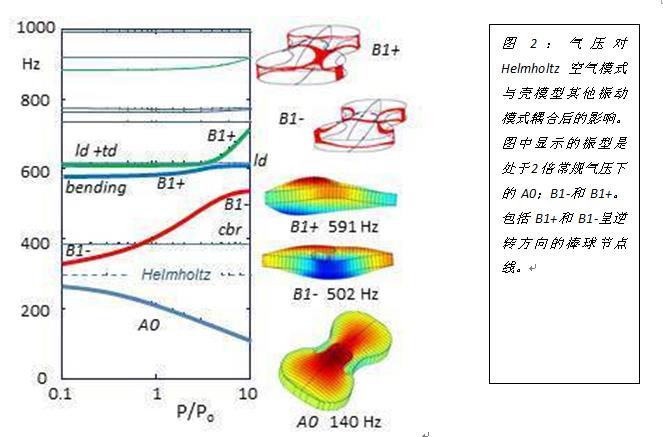 模型上开了音孔能干嘛?简单来说就是振动模式里有多了一种:琴体与亥姆霍兹的耦合共振。在提琴的频谱特征中Helmhotz振动模型被称为A0.(请回忆基础内容中空瓶子吹气的部分)前面小节的有限元仿真中都是在真空环境参数中完成,并没有考虑到腔体内空气的共振。现在开了孔就可以很方便的对比A0与B1-和B1+在耦合与非耦合状态下的关系,如图2所示。
模型上开了音孔能干嘛?简单来说就是振动模式里有多了一种:琴体与亥姆霍兹的耦合共振。在提琴的频谱特征中Helmhotz振动模型被称为A0.(请回忆基础内容中空瓶子吹气的部分)前面小节的有限元仿真中都是在真空环境参数中完成,并没有考虑到腔体内空气的共振。现在开了孔就可以很方便的对比A0与B1-和B1+在耦合与非耦合状态下的关系,如图2所示。
假设一个没有发生耦合的A0是300hz,变量取决于空气中的声速所产生的声压,小提琴内部腔体的体积与F孔的形状。然而任何来自于壳结构的耦合振动都成为一个变量增加了腔体内的空气密度并与常规大气压产生比例关系。如图2所示,哪怕只有十分之一的常规大气压的诱发的压力就会将图表内真空初始阶段的A0和B1-产生强烈的数据分裂与趋势的转向。这些变化来自于helmhozt模式与壳模型的呼吸模式在内外两个方向上的振动耦合作用。
随着空气压的增加,呼吸模式B1-和空气模式A0之间的耦合也增强,导致A0频率降低至远小于没有发生耦合共振时的A0频率。这种耦合也同时导致了B1-频率的增加,呼吸模式的特性在有了空气后显示了出来。在这个阶段的壳模型虽然没有音柱和由其产生的弹性常数代表模式CBR。但是B1-的分裂与频率的转向特性,使得B1-频率曲线在不发生耦合的情况下接近并与高频的模式bending and ld longitudinal dipole发生交集。
通过空气模式与:呼吸模式耦合增强的B1-,bending and ld longitudinal dipole成为横跨琴腰区域的三个主要标准振动模式。三者之间耦合组成的振动模式结构比例不一样。由呼吸模式组合而成的振动模式被三种标准振动模式共享。以上在视频2中可以看到,当壳模型增加了F孔和琴码之后的振动模式。其中的小圆片代表着空气通过F控的运动,用于观测呼吸模式组合后的每一种振动模式的相关情况。
图2中B1-和B1+振动模态图形清楚的显示出由呼吸模式和弯曲模式耦合形成的同相位与异相位振动。图中也显示出跨越面板与背板的,呈逆转状态的棒球节点线。这是在对B1+和B1-进行观测时重要的一种特征,由呼吸模式B1-与弯曲模式B1+的耦合振动形成,存在于所有带有拱形面板的薄壳体结构中。
这种耦合由弯曲波在所有拱形表面上的纵向应变引起。由于面板和背板不完全一样,由弯曲波诱导产生的变化体现在节点线在面板与背板上存在长宽上的差别,耦合的效果在呼吸模式B1-中体现的很明显。这导致了薄壳结构的弯曲现象更像是两片正在做热处理的金属片,会由于热膨胀系数的差异(不同的材料性能)而出现的弯曲现象。在这种耦合作用下,B1-和B1+的共振频率会一直被一个差量分开。这个差值取决于面板与背板由不同拱形诱发的扩展运动的差异。
在较低气压时,只有呼吸模式B1-的频率会随着气压的升高而增加。而其他的高频组合模态都没受到腔体内体积变化的影响。因此在1000hz以下的范围内,A0除了与B1-发生耦合外,并不会与其他组合模态发生耦合,也不会产生显著的单极声辐射贡献。这一点证实了前文中的说法:即在单极特征模式频率范围内,小提琴声辐射都是由呼吸模式直接产生的的,并通过其与Helmoltz空气模式共振耦合间接产生声辐射。其他的振动模式不参与其中,对声辐射没有显著贡献。(Gough,2015b)。
B1-和B1的单极振源强度取决于各自与空气模式和呼吸模式的组成的耦合振动模式。这强烈的依赖于非的耦合状态的的呼吸模式和空气模式。两者之间的振源强度比例与B1-和B1+的声学频谱特征数据呈强相关性,这些变量会体现在每一把不同的琴上。
4.5 真·壳模型:琴码音柱都加上去
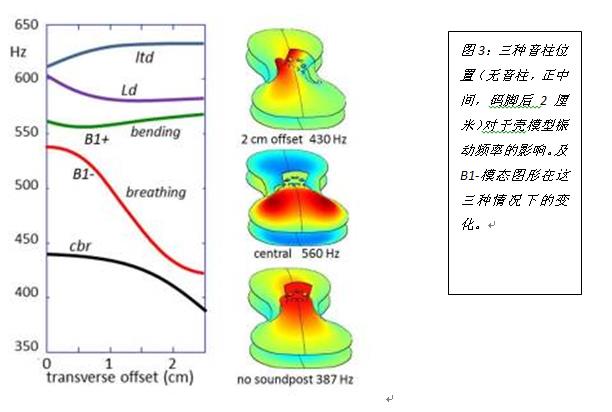
到了这一阶段,终于我们一步步把拆成碎片的琴组装起来。在实际情况下研究小提琴作为一个整体的振动模式。如图3所示,音柱对B1-的呼吸模式组合有特别强的影响。在低频下,一个经过仔细调整过的声柱起着刚性约束的作用,将面板和背板的平面内位移与倾斜运动连接在一起。这引起了图3中B1-曲线在频率上的急剧衰减。
因此,音柱扮演着屏障或闸门的作用,阻止了从音孔下方区域产生的弯曲波通过琴中心岛屿区到达音孔上方区域,反之亦然。当把音柱放到正中间位置时,B1-呼吸模式的声辐射频率从没有音柱的387hz一下子提升到了560hz,正好是一个完美的五分之一音程。处于中央位置的音柱与弯曲模式和纵向偶极模式都发生强烈的相互作用下,导致了图3中振动方向的分裂与转向。视频3说明了从0到2厘米音柱偏移对壳模型的影响。这表明,除了靠近声柱的琴中心岛屿区域外,声柱对最低频率振型的影响相对较弱。
偏移2厘米之后的音柱,使得琴中岛区域与低音侧产生了更大的间隙。这使源自音孔下方区域的呼吸模式振动可以渗透至琴中岛区,穿越并达到更远的区域。这种情况下原有中央音柱的B1频率从560hz下降至430hz。Jansson等人(1970)在早期全息摄影测量中观察到这种模式形状,并在许多后来的实验模态分析测量中验证了这一发现。偏移音柱对于琴中岛区域的呼吸模式产生了强烈的扰动效果,并且可以使其被弓在琴弦上产生平行于面板的力强烈的激发。因此,声音的激发效率很大程度上取决于音柱的位置,而音柱的位置是调试提琴声学性能一个非常重要的因素。
最终请回顾一下本节最开始我们放上的动画,这就是小提琴琴体作为一个整体的低频主要振动模式。也就是所谓频谱特征或典型性振型。(我圈里概念用词严重不统一…)
5. 琴颈,指板与其他配件
琴颈和指板与琴体顶端处于刚性连接状态(就是粘死了的意思)。这一组件的增加,引起了六个新的振动模式,这些模式是由其六个位移和旋转自由度导出的,其频率受支撑颈部的壳体结构的柔性约束。这就产生了六个新的标准模式来表示琴颈部和琴体外壳的内-外耦合振动。声学上最重要的模式是一个悬臂状,琴颈指板与琴体的组合就符合这一模式。这就引入了一种新的壳模型振动模态,通常接近A0共振,也会导致弯曲模式频率略有下降,但对其他壳模式的影响很小。
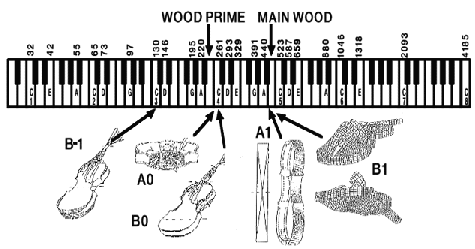
同样,不产生声辐射的振动模态的还包括:拉弦板附近较高频空气纵向振动模态(A1),后小半截琴弦等配件。他们都会在一定程度上与琴体振动模态发生耦合。关于这部分的研究可以参考前文中的图片4 。 但一般情况下,它们的影响将局限于单个共振附近的很小的频率范围,因此只会影响乐器在半音阶或其共振范围内的弯音符部分的声音。有限元仿真的计算中考虑到这部分的因素,并在求解过程中将这些局部对琴体主要振动模态产生的影响体现出来。
REFERENCES:
- Colin E. Gough:《Springer Handbook on Acoustics – String instrument》 P 37-P 74
- Colin E. Gough: [A violin shell model Vibrational modes and acoustics]
- Colin E. Gough:[Supplementary Text Violin Acoustics]
- William F “Jack” Fry《A Physicist’s Quest for the “Secrets” of Stradivari》
- Carleen Hutchins《Research Papers in Violin Acoustics, 1975-1993: With an Introductory Essay 350 Years of Violin Research》
- 维基百科:Violin Acoustics
- 张承忠:[小提琴振动机理及声学品质研究]
- Martin Schleske:[Empirical Tools in Contemporary Violin Making: Part I. Analysis of Design, Materials, Varnish, and Normal Modes]
- Martin Schleske: [ZEITGEIST AND VIOLINMAKING]
- Samuel Zygmuntowicz: Strad3D.org